АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Розділ 9.1. Математичне сподівання неперервної випадкової величини

Читайте также:
  1. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  2. АКУСТИЧНІ ВЕЛИЧИНИ
  3. Величини
  4. Визначення величини резерва сумнівних боргів на основі класифікації дебіторської заборгованості
  5. Вимірювані величини і методи вимірювань
  6. Випадкові величини та їх розподіл
  7. Випадкові події і величини, їх числові характеристики
  8. Висновки до 3 розділу
  9. Відносні статистичні величини, їх види за аналітичною функцією, економічний зміст, методика обчислення та одиниці вимірювання
  10. ВІДЦЕНТРОВІ ПИЛЕОСАДНІІ СУСПЕНЗІЙНО- РОЗДІЛЬНІ АПАРАТИ (ЦИКЛОНИ)
  11. Властивості математичного сподівання
  12. Вплив величини напруги і параметрів ланцюга на перехідний процес

Нехай неперервна випадкова величина Х задана диференціальною

функцією f(х).

Припустимо, що всі значення Х належать відрізку [a,b]. Розіб’ємо цей відрізок на m частин Δх1, Δх2,.. Δхn, які не перетинаються і 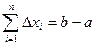. Виберемо на кожному з елементарних відрізків по одній точці 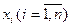). Користуючись формулою математичного сподівання для дискретної випадкової величини, запишемо наближене значення математичного сподівання величини

 

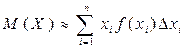. (9.1)

 

Суму (9.1) можна розглядати, як інтегральну суму, тому, переходячи до границі при 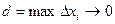отримаємо формулу математичного сподівання неперервної випадкової величини

.

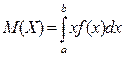Означення: Математичним сподіванням неперервної випадкової величини Х, можливі значення якої належать відрізку 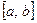, називають визначений інтеграл

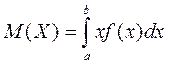. (9.2)

 

Якщо неперервна випадкова величина задана на всій числовій осі, тобто 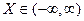, тоді

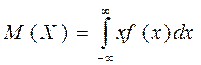. (9.3)

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)