 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Закон рівномірного розподілу ймовірностей
 Означення: Розподіл ймовірностей називається рівномірним, якщо на інтервалі, якому належать всі можливі значення випадкової величини, диференціальна функція має стале значення
Означення: Розподіл ймовірностей називається рівномірним, якщо на інтервалі, якому належать всі можливі значення випадкової величини, диференціальна функція має стале значення
 (10.6)
(10.6)
 Приклад:
Приклад:
Шкала вимірювального пристрою поділена в деяких одиницях. Помилку при округленні відрахування до найближчої цілої поділки можна розглядати як випадкову величину Х, яка може приймати із сталою щільністю ймовірності будь-яке значення між двома сусідніми цілими поділками.
 Диференціальна функція рівномірного розподілу
Диференціальна функція рівномірного розподілу
Знайдемо диференціальну функцію рівномірного розподілу, вважаючи, що всі можливі значення випадкової величини Х належать інтервалу  , на якому диференціальна функція зберігає стале значення
, на якому диференціальна функція зберігає стале значення 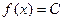 .
.
Для  та
та  ,
, 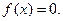
Тому  .
.
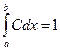 ,
, 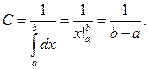
Враховуючи вищевикладене, закон рівномірного розподілу можна записати у вигляді
 (10.7)
(10.7)
 Інтегральна функція рівномірного розподілу
Інтегральна функція рівномірного розподілу
Знайдемо інтегральну функцію рівномірного розподілу
 .
.
При  ,
,  , а
, а 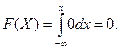
При  ,
, 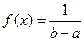 , а
, а 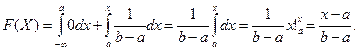
При 
 а
а 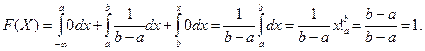
Тоді інтегральна функція рівномірного розподілу набуде вигляду
 (10.8)
(10.8)
Поиск по сайту: