Задачі до розділу 4.1

Задача 4.1.1

В ящику 30 виробів: 20 стандартних і 10 підвищеної якості. Витягли підряд 4 вироба, причому кожний вироб повертали назад до ящика перед вилученням другого і вироби в ящику змішувалися. Яка ймовірність того, що серед вилучених 4 виробів будуть 2 стандартні?

Рішення

Ймовірність вилучення стандартного виробу можна вважати однаковою у всіх чотирьох випробуваннях. Тоді ймовірність протилежної події (вилучення виробу підвищеної якості) дорівнює . Використовуючи формулу Бернуллі (4.1), одержимо:

Задача 4.1.2

Ймовірність появи події А дорівнює 0,4. Яка ймовірність того, що при 10 випробуваннях подія А з’явиться не більше 3 раз?

Рішення.

З умови задачі:

Ймовірність появи події А 0 раз:

Ймовірність появи події А 1 раз: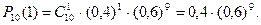

Ймовірність появи події А 2 рази:

Ймовірність появи події А 3 рази:

Ймовірність того, що подія А з’явиться не більше 3 раз, визначається із виразу

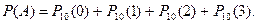
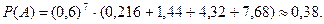
Задача 4.1.3

Обчислити ймовірність появи події А рівно 3 рази у 7 випробуваннях, якщо ймовірність появи події у кожному випробуванні однакова і дорівнює 0,6.

Задача 4.1.4

Ймовірність купівлі одиниці бракованого товару дорівнює 0,1. Знайти ймовірність того, що з 7 куплених одиниць товару 5 буде без браку.

Задача 4.1.5

Визначити ймовірність того, що у родині, яка має шестеро дітей, буде 2 хлопчика і чотири дівчинки. Ймовірність народження хлопчика вважати рівною 0,51.

Задача 4.1.6

Два рівносильних гравця грають у шахи. Що є більш вірогідним:

а) виграти одну партію з двох або дві партії з чотирьох?

б) виграти не менше двох партій з чотирьох або не менше трьох партій з п’яти? Вважати, що нічийний результат не береться до уваги.

Задача 4.1.7

Пристрій складається з трьох основних незалежно працюючих елементів. Пристрій не працює, якщо відмовиться працювати хоча б один його елемент. Ймовірність відмови кожного елемента за певний час дорівнює 0,2. Знайти ймовірність безвідмовної роботи пристрою за певний час, якщо:

а) працюють тільки основні елементи;

б) підключено один резервний елемент;

в) підключено два резервних елемента.

Припускається, що резервні елементи працюють у тому ж режимі, що і основні. Ймовірність відмови кожного резервного елемента дорівнює 0,2 і пристрій не працює, коли працює менше трьох елементів.

Розділ 4.2. Локальна теорема Лапласа

Легко бачити, що в разі великих значень п користуватися формулою Бернуллі достатньо важко. Наприклад, якщо 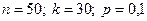, тоді за формулою (4.1) і необхідно зробити обчислення ,які є досить обтяжливими. Тому існує формула, яка дозволяє наближено знайти ймовірність того, що при п випробуваннях подія А з’явиться рівно раз, якщо число іспитів достатньо велике.

Цю асимптотичну формулу для р =0,5 було знайдено у 1730 році Муавром, а у 1783 році Лаплас узагальнив її для довільної р, відмінної від 0 та 1, тому іноді її називають теоремою Муавра-Лапласа.

Теорема: Якщо ймовірність р появи події А в кожному випробуванні постійна і відмінна від нуля і одиниці, тоді ймовірність того, що подія А з’явиться в п випробуваннях рівно k раз, наближено дорівнює (тим точніше, чим більше п) значенню функції

, (4.2)

при .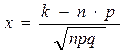

Існують таблиці, в яких розміщені значення функції 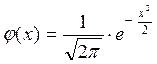, які відповідають додатнім значенням аргументу . Для від’ємних значень аргументу користуються тією ж таблицею, оскільки функція є парною, тобто .

Приклад:

Знайти ймовірність того, що подія А з’явиться рівно 80 раз у 400 випробуваннях, якщо ймовірність появи цієї події у кожному випробуванні дорівнює 0,2.

Поиск по сайту: