АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Розділ 5.1. Інтегральна теорема Лапласа

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Висновки до 3 розділу
  3. ВІДЦЕНТРОВІ ПИЛЕОСАДНІІ СУСПЕНЗІЙНО- РОЗДІЛЬНІ АПАРАТИ (ЦИКЛОНИ)
  4. Внешние эффекты (экстерналии). Теорема Коуза.
  5. Внешние эффекты, их виды и последствия. Теорема Коуза
  6. Вопрос 1 теорема сложения вероятностей
  7. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  8. Вопрос. Теорема Котельникова (Найквиста)
  9. Вставка розриву сторінки або розділу
  10. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  11. Гранична теорема Пуассона
  12. Демультиплексор (роздільник) Demux

 

Теорема: Якщо ймовірність р появи події А в кожному випробуванні постійна і відмінна від нуля і одиниці, тоді ймовірність того, що подія А відбудеться у п випробуваннях від k1 до k2 раз, наближено дорівнює визначеному інтегралу

 

, (5.1)

 

де .

 

 

Позначимо , де - є непарною функцією, тобто , що знаходиться за допомогою таблиці функції Лапласа, причому, якщо 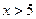, тоді . Враховуючи вищевикладене одержуємо

 

 

.

 

Значить

. (5.2)

 

 

Приклад:

Ймовірність виходу з ладу одного верстата за одну зміну дорівнює 0,2. Знайти ймовірність того, що протягом однієї зміни від 20 до 25 верстаті будуть працювати безвідмовно, якщо в цій зміні працює 30 верстатів.

 

Рішення

 

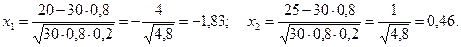
За таблицею функції Лапласа

 

 

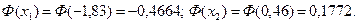
Використовуючи формулу (5.2) маємо

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)