 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
Величина d Ф 
= E 
dS= E d S называется потоком вектора напряженности через площадку d S. Здесь d S = dS n — вектор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке. Выбор направления вектора n (а, следовательно, и d S) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — 1 В× м.
Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверхность
Ф = 
= 
,
Поток вектора Е является алгебраической величиной и зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватываемой поверхностью.
Вычисление напряженности поля системы электрических зарядов можно значительно упростить, используя теорему Остроградского-Гаусса.
Поток вектора напряженности сквозь сферическую поверхность радиуса r, охватывающую точечный заряд Q, находящийся в ее центре равен
Ф = = 
= 
.
Этот результат справедлив для замкнутой поверхности любой формы.
В общем случае произвольной поверхности, окружающей п зарядов, в соответствии с принципом суперпозиции, напряженность. Е поля равна сумме напряженностей Е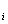 
полей, создаваемых каждым зарядом в отдельности: Е = 
. Поэтому Ф = = 
= 
.
Каждый из интегралов, стоящий под знаком суммы, равен Q /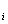 
. Следовательно,
= =  
| (3.11) |
Уравнение выражает теорему Остроградского-Гаусса для электростатического поля в вакууме: поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на εо. Эта теорема доказана для векторного поля любой природы русским математиком М. В. Остроградским (1801—1862), а затем независимо от него применительно к электростатическому полю — К. Гауссом.
В общем случае электрические заряды могут быть распределены в пространстве с непостоянной объемной плотностью ρ = dQ/dV. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, охватывающей некоторый объем V,
= 
| (3.12) |
и теорему Гаусса (3.11) можно записать так: 
= = 
.
1. Поле равномерно заряженной бесконечной плоскости. Бесконечная плоскость заряжена с постоянной поверхностной плотностью + 
( =dQ/dS— заряд, приходящийся на единицу поверхности).
Поиск по сайту: