 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 13 Идеальный газ
Для вывода основного уравнения молекулярно-кинетической теории рассмотрим идеальный одноатомный газ. Предположим, что молекулы газа движутся хаотически, число взаимных столкновений между молекулами газа пренебрежимо мало по сравнению с числом ударов о стенки сосуда, а соударения молекул со стенками сосуда абсолютно упругие. Выделим на стенке сосуда некоторую элементарную площадку S (рисунок 2.5) и вычислим давление, оказываемое на эту площадку.
При каждом соударении молекула, движущаяся перпендикулярно площадке, передает ей импульс
| m0v–(–m0v)=2m0v, | (2.21) |
где m0 – масса молекулы, v – ее скорость. За время t площадки S достигнут только те молекулы, которые заключены в объеме цилиндра с основанием S и высотой v t (рисунок 2.5). Число этих молекул равно n Sv t (n – концентрация молекул).
Необходимо учитывать, что реально молекулы движутся к площадке S под разными углами и имеют различные скорости, причем скорость молекул при каждом соударении меняется. Для упрощения расчетов хаотическое движение молекул заменяют движением вдоль трех взаимно перпендикулярных направлений, так что в любой момент времени вдоль каждого из них движется 1/3 молекул. Половина этих молекул (т.е. 1/6 часть) движется вдоль данного направления в одну сторону, а вторая половина – в противоположную. Тогда число ударов молекул, движущихся в заданном направлении, о площадку S будет 1/6 n Sv t. При столкновении с площадкой эти молекулы передадут ей импульс
| P = 2m0v1/6nSvt = 1/3nm0v2St | (2.22) |
Тогда давление газа, оказываемое им на стенку сосуда,
| P = P/(tS) = 1/3nm0v2. | (2.23) |
Если газ в объеме V содержит N молекул, движущихся со скоростями v1, v2,..., vN, то целесообразно рассматривать среднюю квадратичную скорость
<vкв>= 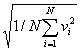 , ,
| (2.24) |
характеризующую всю совокупность молекул газа. Уравнение (2.23) с учетом (2.24) примет вид
| p = 1/3nm0<vКВ>2. | (2.25) |
Выражение (2.25) называется основным уравнением молекулярно-кинетической теории идеальных газов.
| PVm = RT |
Уравнению
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа, называемым также уравнением Клапейрона – Менделеева.
В молекулярно-кинетической теории пользуются моделью идеального газа, согласно которой считают, что:
1) собственный объем молекул газа пренебрежимо мал по сравнению с объемом сосуда;
2) между молекулами газа отсутствуют силы взаимодействия;
3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов в условиях, близких к нормальным (например, кислород и гелий), а также при низких давлениях и высоких температурах.
Поиск по сайту: