Вопрос 8 Момент инерции твердого тела

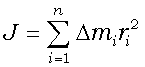Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси:

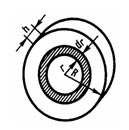
Рисунок 1.18 -

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1.18). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и массой dm. Момент инерции каждого такого цилиндра dJ = r ² dm (так как dr << r, то считаем, что расстояние всех точек цилиндра от оси равно r). Если ρ – плотность материала, объем 2πrhdr, то dm=2πrhρdr и dJ = 2πhρr³dr. Тогда момент инерции сплошного цилиндра

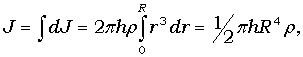
но так как 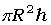– объем цилиндра, то его масса 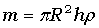, а момент инерции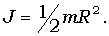

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции J _с относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы т тела на квадрат расстояния а между осями:

Поиск по сайту: