Вопрос 63 Волновая функция

Экспериментальное подтверждение идеи де Бройля об универсальности корпускулярно-волнового дуализма, ограниченность применения классической механики к микрообъектам, диктуемая соотношением неопределенностей, а также противоречие целого ряда экспериментов с применяемыми в начале XX в. теориями, привели к новому этапу развития квантовой теории - созданию квантовой механики, описывающей законы движения и взаимодействия микрочастиц с учетом их волновых свойств.Ее создание и развитие охватывает период с 1900 г. (формулировка Планком квантовой гипотезы) до 20-х годов XX в.; оно связано прежде всего с работами австрийского физика Э. Шредингера (1887—1961), немецкого физика В. Гсйзенберга и английского физика П. Дирака (1902—1984).

На данном этапе развития возникли новые принципиальные проблемы, в частности проблема физической природы волн де Бройля. Для выяснения этой проблемы сравним дифракцию световых волн и микрочастиц. Дифракционная картина, наблюдаемая для световых волн, характеризуется тем, что в результате наложения дифрагирующих волн друг на друга в различных точках пространства происходит усиление или ослабление амплитуды колебаний. Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. По представлениям фотонной теории, интенсивность определяется числом фотонов, попадающий в данную точку дифракционной картины. Следовательно, число фотонов в данной точке дифракционной картины задается квадратом амплитуды световой волны, в то время как для одного фотона квадрат амплитуды определяет вероятность попадания фотона в ту или иную точку.

Дифракционная картина, наблюдаемая для микрочастиц, также характеризуется неодинаковым распределением потоков микрочастиц, рассеянных или отраженных по различным направлениям, - в одних направлениях наблюдается большее число частиц, чем в других. Наличие максимумов в дифракционной картине с точки зрения волновой теории означает, что эти направления соответствуют наибольшей интенсивности волн де Бройля. С другой стороны, интенсивность волн де Бройля оказывается больше там, где имеется большее число частиц, т.е. интенсивность волн де Бройля в данной точке пространства определяет число частиц, попавших в эту точку. Таким образом, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

Необходимость вероятностного подхода к описанию микрочастиц является важнейшей отличительной особенностью квантовой теории. Можно ли волны де Бройля истолковывать как волны вероятности, т.е. считать, что вероятность обнаружить микрочастицу в различных точках пространства меняется по волновому закону? Такое толкование волн де Бройля уже неверно хотя бы потому, что тогда вероятность обнаружить частицу в некоторых точках пространства может быть отрицательна, что не имеет смысла.

Чтобы устранить эти трудности, немецкий физик М. Борн (1882—1970) в 1926 г. предположил, что по волновому закону меняется не сама вероятность, а величина, названная амплитудой вероятности и обозначаемая 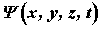Эту величину называют. также волновой функцией (или 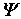- функцией). Амплитуда вероятности может быть комплексной, и вероятность пропорциональна квадрату ее модуля:

(6.46)

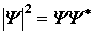( , - функция, комплексно сопряженная с 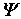). Таким образом, описание состояния микрообъекта с помощью волновой функции имеет статистический, вероятностный характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в момент времени ,в области с координатами и , и , и .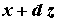

Итак, в квантовой механике состояние микрочастиц описывается принципиально по-новому - с помощью волновой функции, которая является основным носителем информации об их корпускулярных и волновых свойствах. Вероятность нахождения частицы в элементе объемом равна

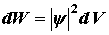
(6.47)

Величина

(квадрат модуля 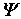- функции) имеет смысл плотности вероятности, т. е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами . Таким образом, физический смысл имеет не сама 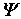- функция, а квадрат ее модуля 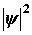, которым задается интенсивность волн де Бройля.

Вероятность найти частицу в момент времени в конечном объеме , согласно теореме сложения вероятностей, равна

.

Так как определяется как вероятность, то необходимо волновую функцию 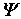нормировать так, чтобы вероятность достоверного события обращалась в единицу, если за объем принять бесконечный объем всего пространства. Это означает, что при данном условии частица должна находиться где-то в пространстве. Следовательно, условие нормировки вероятностей

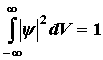(6.48)

где данный интеграл (6.48) вычисляется по всему бесконечному пространству, т. е. по координатам от до . Таким образом, условие (6.48) говорит об объективном существовании частицы в пространстве.

Чтобы волновая функция являлась объективной характеристикой состояния микрочастиц, она должна удовлетворять ряду ограничительных условий. Функция 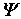, характеризующая вероятность обнаружения действия микрочастицы в элементе объема, должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком).

Волновая функция удовлетворяет принципу суперпозиции: если система может находиться в различных состояниях, описываемых волновыми функциями 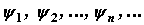, то она также может находиться в состоянии 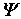, описываемом линейной комбинацией этих функций:

,

Где - произвольные, вообще говоря, комплексные числа. Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей.

Волновая функция 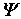, являясь основной характеристикой состояния микрообъектов, позволяет в квантовой механике вычислять средние значения физических величин, характеризующих данный микрообъект. Например, среднее расстояние электрона от ядра вычисляют по формуле

,

где интегрирование производится, как и в случае (6.48).

Поиск по сайту: