 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Вопрос 43 Закон полного тока
Циркуляцией вектора В по заданному замкнутому контуру называется интеграл
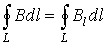
где dl — вектор элементарной длины контура, направленной вдоль обхода контура, Bl=Bcosa — составляющая вектора В в направлении касательной к контуру (с учетом выбранного направления обхода), a — угол между векторами В и d l.
Закон полного тока для магнитного поля в вакууме: циркуляция вектора В по произвольному замкнутому контуру равна произведению магнитной постоянной m0 на алгебраическую сумму токов, охватываемых этим контуром:

| (4.9) |
где n — число проводников с токами, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается контуром.
Внутри соленоида поле является однородным, а снаружи — неоднородным и очень слабым.
Для магнитной индукции поля внутри соленоида (в вакууме):
| B=m0 NI / l |
B=m0NI/(2pr), где N — число витков тороида.
Если контур проходит вне тороида, то токов он не охватывает и В×2pr=0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).
Поиск по сайту: