S-M-N-теорема, приклади її використання

Теорема 4 (s-m-n -теорема). Для довiльних m, n >1 iснує (m +1)- арна РФ s (z, x ₁, ..., x_m), така, що для всiх z, x ₁, ..., x_т, у ₁ ,..., у_п j (x ₁ ,..., x_т, у ₁ ,..., у_п) =j (у ₁ ,..., у_п).

Приклад 1. Залежнiсть функцiї s вiд n можна зняти, якщо для завдання ЧРФ використати МТ.

Справді, за z визначаємо МТ із кодом z для функцiї j . Задамо нову МТ M, яка злiва вiд початкового вмiсту стрiчки дописує слово , a далi моделює роботу МТ із кодом z. Така МТ M при входi обчислює n -арну функцiю j , причому k - код МТ M - не залежить вiд n.

Теорема 5 (s - m - n -теорема в спрощенiй формi). Для кожної ЧРФ f (x ₁ ,..., x_т, у ₁ ,..., у_п) iснує РФ s (x ₁, ..., x_m) така, що для всiх x ₁, ..., x_т, у ₁ ,..., у_п маємо f (x ₁ ,..., x_т, у ₁ ,..., у_п) = j (у ₁ ,..., у_п).

При т=п= 1 спрощена s - m - n -теорема формулюється так:

Теорема 6. Для кожної ЧРФ f (x, y) iснує РФ s (x) така, що для всiх значень x, y маємо f (x, y)= j _{s (x)}(y).

Розглянемо приклади застосування s - m - n -теореми.

Приклад 2. Існує РФ s (x, y) така, що для всіх х, y, z Î N маємо j _{s ( x , y )}(z)=j _x (z)+j _y (z).

Розглянемо функцію f (x, y, z) = j _x (z) + j _y (z). Функція f є ЧРФ, тому за s - m - n -теоремою існує РФ s (x, y) така, що для всіх х, y, z Î N маємо f (x, y, z)=j _{s ( x , y )}(z)=j _x (z)+j _y (z).

Приклад 3. Для кожної 1-арної ЧРФ f існує РФ s (x), така, що для всіх х Î N маємо D_{s ( x )}= f ^-1(D_x).

Розглянемо функцію g (x, y) = j _x (f (y)). Така функція є ЧРФ за ТЧ, тому за s - m - n -теоремою існує РФ s (x) така, що для всіх х, y Î N g (x, y) = j _{s ( x )}(у). Зафіксуємо х. Mаємо

у Î D_{s ( x )} Û j _{s ( x )}(у)¯ Û g (x, y)¯ Û j _x (f (y))¯ Û f (y)Î D_x Û y Î f ^-1(D_x).

Звідси D_{s ( x )}= f ^-1(D_x).

Приклад 4. Існує РФ s (x) така, що для всіх х Î N маємо Е_{s ( x )}= D_x.

Розглянемо функцію f (x, y)= Така функція є ЧРФ за ТЧ, тому за s - m - n -теоремою існує РФ s (x) така, що для всіх х, y Î N маємо f (x, y)=j _{s ( x )}(у). Зафіксуємо х. За побудовою функції f маємо D_{s ( x )}= Е_{s ( x )}. Тепер у Î Е_{s ( x )} Û у Î D_{s ( x )} Û j _{s ( x )}(у)¯ Û f (x, y)¯ Û у Î D_x.

Звідси Е_{s ( x )}= D_x.

Приклад 5. Існує РФ t (x) така, що для всіх х Î N маємо D_{t ( x )}= Е_x.

Розглянемо функцію f (x, y)= Така функція є ЧРФ за ТЧ, тому за s - m - n -теоремою існує РФ t (x) така, що для всіх х, y Î N f (x, y)=j _{t ( x )}(у). Зафіксуємо х. Mаємо у Î D_{t ( x )} Û j _{t ( x )}(у)¯ Û f (x, y)¯ Û у Î E_x. Звідси D_{t ( x )}= E_x.

Приклад 6. Існує РФ s (x) така, що для всіх х Î N маємо

={(u, v) | x =2 u +3 v }.

Розглянемо функцію f (x, u, v)=

За ТЧ f є ЧРФ, тому за s - m - n -теоремою існує РФ s (x) така: для всіх х, u, v Î N f (x, u, v)= 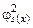(u, v). Зафіксуємо х. Тепер

(u, v)Î Û 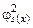(u, v)¯ Û f (x, u, v)¯ Û x =2 u +3 v.

Звідси ={(u, v) | x =2 u +3 v }.

Приклад 7. Існує РФ s (x, y) така, що для всіх х, y Î N маємо D_{s ( x , y )}= D_x È D_y.

Розглянемо функцію f (x, y, z)= Така функція є ЧРФ за ТЧ, тому за s - m - n -теоремою існує РФ s (x, y) така, що для всіх х, y, z Î N маємо f (x, y, z)= =j _{s ( x , y )}(z). Зафіксуємо х та y. Маємо

z Î D_{s ( x , y )} Û j _{s ( x , y )}(z)¯ Û f (x, y, z)¯ Û z Î D_x È D_y.

Звідси випливає D_{s ( x , y )}= D_x È D_y.

Приклад 8. Існує РФ s (x, y) така, що для всіх х, y Î N маємо D_{s ( x , y )}= Е_{s ( x , y )}= D_x Ç D_y.

Розглянемо функцію f (x, y, z)= Така функція є ЧРФ за ТЧ, тому за s - m - n -теоремою існує РФ s (x, y) така, що для всіх х, y, z Î N маємо f (x, y, z)=j _{s ( x , y )}(z). Зафіксуємо х та y. За побудовою функції f маємо D_{s ( x , y )}= Е_{s ( x , y )}. Тепер

z Î Е_{s ( x , y )} Û z Î D_{s ( x , y )} Û j _{s ( x , y )}(z)¯ Û f (x, y, z)¯ Û z Î D_x Ç D_y.

Звідси отримуємо D_{s ( x , y )}= Е_{s ( x , y )}= D_x Ç D_y.

ЛЕКЦІЯ 10

ПЛАН

1. Теореми Кліні про нерухому точку.

1. Теореми Кліні про нерухому точку

Теорема 1. Нехай f - (n +1)- арна РФ. Тодi iснує n-арна РФ g, така, що для всiх значень x ₁,..., x_п маємо j = j .

За s - m - n -теоремою iснує РФ s (и, x ₁, ..., x_п) така, що для всiх u, x ₁,..., x_п, y маємо

j = j . (1)

Нехай функцiя f (s(x ₁,..., x_п), x ₁,..., x_п) має iндекс k у нумерацiї (n +1)-арних ЧРФ, тобто це функцiя j 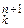( u, x ₁,..., x_п). За тотальнiстю функцiй f та s функцiя j 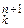тотальна. Тому при u = k для всiх x ₁,..., x_п маємо

f (s(x ₁,..., x_п), x ₁,..., x_п) = j 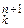(k, x ₁,..., x_п). (2)

Iз (1) при u = k та iз (2) дiстаємо

j = j = j

для всiх x ₁,..., x_п . Отже, функцiя g (x ₁,..., x_п)= s (k, x ₁,..., x_п) - шукана РФ.

Для випадку n =0 теорема 1 переформульовується так:

Теорема 2. Нехай f (x) - РФ. Тодi iснує n Î N таке, що j _n = j _{f (n)}.

Наведену теорему Клiнi про нерухому точку краще називати теоремою про псевдонерухому точку. Справдi, умова j _n= j _{f (n)} зовсiм не означає, що n = f (n), a свiдчить тiльки про те, що n i f (n) - iндекси одної i тої ж ЧРФ.

Теорему про нерухому точку називають також теоремою про рекурсiю, бо вона виражає рекурсивне визначення дуже загального вигляду. Наприклад, визначимо функцiю j _n через задану РФ f так: j _n= j _{f (n)} . Тодi j _n ефективно визначена через n - код МНР-програми для її обчислення, бо таке n iснує згiдно з теоремою 2.

Наслiдок 1. Нехай f (x) - РФ. Тодi iснує n Î N таке, що D_n = D_f(n) та E_n = E_f(n).

Справдi, згiдно з теоремою 2 досить узяти n Î N таке, що j _n = j _f(n).

Наслiдок 2. Нехай h (z, x) - ЧРФ. Тодi iснує n Î N таке, що для всiх x h (n, x) = j _n (x).

За s - m - n -теоремою iснує РФ s (z) така, що h (z, x) = j _{s (z)}(x) для всiх z, x. За теоремою 2 iснує таке n, що j _n = j _s(n) , тобто h (n, x) = j _s(n) (x) = j _n (x)для всiх x.

Зауважимо, що формулювання наслідку 2 - це первісне формулювання самого С.Кліні теореми про нерухому точку. Покажемо, що наслідок 2 та теорема 2 еквівалентні. Для цього виведемо теорему 2 із наслідку 2.

Нехай f (x) - РФ. Тоді за тезою Чорча функція h (z, x)=j _g(z) (x) є ЧРФ. За наслідком 2 існує n Î N таке, що для всiх x h (n, x) = j _n (x), тобто для всiх x h (п, x) = j _g(п) (x) = j _n (x).

МНР-програма P самотворна, якщо для довiльного x Î N маємо P (x)¯t(P), де t(P) - код програми P. На перший погляд, таких програм бути не може, бо для побудови P треба знати t(P), тобто саму програму P. Проте самотворнi програми таки iснують!

Теорема 3. Існує МНР-програма P така, що P (x)¯t(P) для всiх значень x.

Вiзьмемо функцiю h (z, x) = z. За наслiдком 2 iснує таке n, що для всiх x h (n, x) = j _n (x). Отже, j _n (x) = h (n, x) = n для всiх x. Тому програма P із кодом n - шукана.

Покажемо тепер, що нерухома точка кожної РФ j _n ефективно залежить вiд її iндексу n. Це посилює твердження теореми 2.

Теорема 4. Існує РФ a(x) така: для кожного n Î N, якщо j _n є РФ, то j_a(n) = .

За s - m - n -теоремою iснує РФ s (x) така, що

= j _{s (x)}(y)для всiх x, y Î N. (1)

Тодi за s - m - n -теоремою iснує РФ n (x), для якої

j _n (s (x)) = j _{n (n)}(x) для всiх n, x Î N. (2)

Якщо j _n є РФ, то кожне значення j _n (x) визначене. Взявши x = n (n), iз (1) маємо

j _{s ( n (n))} (3)

та iз (2) маємо j _n (s (n (n))) = j _{n (n)}(n (n)). Звiдси та із (3) дiстаємо j _{s ( n (n))}= . Поклавши a(x)= s (n (x)), маємо j_a(n) = .

Покажемо, що для кожної РФ можна ефективно знайти монотонно зростаючу послiдовнiсть її нерухомих точок. Звiдси, зокрема, випливає нескiнченнiсть множини нерухомих точок кожної РФ.

Теорема 5. Для кожної РФ f (x) iснує строго монотонна РФ a(x), така, що для кожного n Î N маємо j_a(n)=j _{f (a(n))}.

За s - m - n -теоремою iснує РФ s (x) така: j _{s (x)}(y)для всiх x, y Î N. Нехай m - деякий iндекс функцiї s (x), тобто s (x) – суть j _m (x). Звiдси для всiх y Î N, тобто j _m (m) - нерухома точка функцiї f. Згiдно із зауваженням 1 до s - m - n -теореми s (x)³ x для всiх x Î N, тому j _m (m)³ m.

Функцiю a(x) задамо так:

- a(0)= , де m ₀ – довiльний iндекс функцiї s;

- a(k +1)= , де m_{k+ 1} - такий iндекс функцiї s, що m_{k+ 1}>a(k)

(у силу твердження 1 такий iндекс знаходиться ефективно).

Кожне значення функцiї a є нерухомою точкою функцiї f. Функцiя a алгоритмiчно обчислювана, вона тотальна в силу тотальностi функцiї s. За ТЧ a є РФ, причому для всiх k Î N a(k +1)= ³ m_{k+ 1}>a(k). Тому a - строго монотонна РФ.

Наслiдок. Для кожних РФ f (x) та k Î N iснує n Î N таке, що n>k та j _n =j _{f (n)}.

Розглянутi нами ефективнi нумерацiї ЧРФ неоднозначнi. Однозначнi ефективні нумерацiї ЧРФ iснують, але немає в певному смислi "природних" однозначних ефективних нумерацiй ЧРФ.

Теорема 6. Нехай f (x) - строго монотонна тотальна функцiя, для якої виконуються умови:

1) якщо m ¹ n, то j _{f (т)}¹j _{f (n)};2) f (n) - найменший iндекс функцiї j _{f (n)} .

Тодi функцiя f не є ЧРФ.

Функцiя f не може бути тотожною, бо тодi з умови m ¹ n випливає j _m ¹j _n . Тому iснує таке k Î N, що f (n)> n при n ³ k. Але f (n)- найменший iндекс функцiї j _{f (n)} , тому j _{f (т)} ¹ j _{f (n)} для всіх n ³ k. Якщо f рекурсивна, то за наслiдком теореми 5 iснує n Î N таке, що n > k і j _{f (n)}=j _n . Дiстали суперечнiсть, тому функцiя f не є РФ та не є ЧРФ.

Спiльної нерухомої точки для двох довiльних РФ може не бути. Нехай a і b - рiзнi РФ, нехай k і m - iндекси функцiй a і b, тобто a=j _k та b=j _m . Вiзьмемо функцiї-константи f (x)= k і g (x)= m. Якщо iснує спiльна нерухома точка n для f і g, то j _n = j _{f (n)} та j _n = j _{g (n)}. Звiдси a=j _k =j _{f (n)}=j _n =j _{g (n)}= j _m = b, що суперечить припущенню a ¹ b.

Проте можна знайти пару ефективно зв’язаних нерухомих точок для пари заданих РФ:

Теорема 7 (про парну рeкурсiю). Для кожної пари РФ f (x) і g (x) iснують m, n Î N такi, що j _m = j _{f (C (m,n))} та j _n = j _{g (C (m,n))} .

За s - m - n -теоремою iснує РФ s (x, y) така:

j _{f (C (x,y))}(z) = j _{s (x,y)}(z) для всiх x, y, z Î N. (1)

За теоремою 1 для РФ s (x, y) iснує РФ a(y) така, що j_a(y) = j _{s (a(y) ,y)} для всiх y Î N. Ураховуючи (1), звiдси маємо:

j_a(y) = j _{f (C (a(y) ,y))} для всiх y Î N. (2)

За s - m - n -теоремою iснує РФ k (y) така:

j _{g (C (a(y) ,y))}(z)= j _{k (y)}(z) для всiх y, z Î N. (3)

За теоремою 2 для РФ k (y) iснує n Î N таке, що j_n = j _k(n). Звiдси, враховуючи (3), маємо j _n = j _{g (C (a( п ), п ))}. Покладемо m =a(n). Тодi з j _n = =j _{g (C (a(п) ,п))} при y = n дістаємо j _n = j _{g (C (т,п))} та з (2) при y = n маємо j _т =j_a(т) = j _{f (C (a(п) ,п))} = j _{f (C (т,п))} .

ЛЕКЦІЯ 11

ПЛАН

1. Поняття примітивно рекурсивної, рекурсивної та рекурсивно перелічної множини (ПРМ, РМ і РПМ).

2. Еквівалентні визначення РПМ.

3. Властивості ПРМ, РМ та РПМ.

1. Поняття примітивно рекурсивної, рекурсивної і рекурсивно перелічної множини (ПРМ, РМ та РПМ)

Множину M Í Nⁿ називають рекурсивною (скорочено РМ), якщо її характеристична функцiя c _M рекурсивна.

Множину M Í Nⁿ називають примiтивно рекурсивною (скорочено ПРМ), якщо її характеристична функцiя c _M примiтивно рекурсивна.

Зрозумiло, що кожна ПРМ є рекурсивною множиною.

Множину M Í N називають рекурсивно перелiчною (скорочено РПМ), якщо M =Æ або M = E_f для деякої рекурсивної функцiї f.

Множину M Í Nⁿ називають РПМ, якщо M =Æ або iснують 1-арнi РФ g ₁,..., g_n такi, що M ={(g ₁(x),..., g_n (x)) | x Î N }.

Як наслiдки тези Чорча дiстаємо такi твердження:

- клас РМ збігається з класом алгоритмiчно розв’язних множин натуральних чисел;

- клас РПМ збігається з класом алгоритмiчно перелiчних множин натуральних чисел.

Для кожної L Í Nⁿ визначимо множину-згортку

Cⁿ (L)={ Cⁿ (x ₁,..., x_n) | (x ₁,..., x_n)Î L }.

Нехай L Í Nⁿ та M Í Nⁿ. Безпосередньо iз визначень випливає:

Cⁿ (L È M)= Cⁿ (L)È Cⁿ (М), Cⁿ (L Ç M)= Cⁿ (L)Ç Cⁿ (М), Cⁿ (Nⁿ \ L)= N \ Cⁿ (L).

Поиск по сайту: