Теорема про представлення операції примітивної рекурсії

Покажемо, що кодування за допомогою функцiї Геделя G (x, y) довiльних скiнченних послiдовностей натуральних чисел одним натуральним числом дозволяє при розширеннi множини базових функцiй промоделювати операцiю примiтивної рекурсiї.

Теорема. Функцiя f = R (g, h) може бути отримана iз функцiй g, h, базових функцiй і функцiй +, ´ 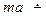за допомогою скiнченної кiлькостi застосувань операцiй суперпозицiї S ^{n+ 1} та мiнiмiзацiї М.

Доводимо для випадку, коли f = R (g, h) - бiнарна функцiя (в загальному випадку доведення аналогiчне).

Зафiксуємо x та y. Згiдно зі схемою примітивної рекурсії для функцiї f (x, y) маємо:

f (x,0) = g (x);

f (x,1) = h (x,0, f (x,0)); (1)

... f (x, y) = h (x, y -1, f (x, y -1)).

За основною властивiстю функцiї Геделя iснує таке t, що

G (t, 0) = f (x,0);

... (2) G (t, y) = f (x, y).

Ураховуючи (1), перепишемо (2) у виглядi

G (t, 0) = g (x);

G (t, 1) = h (x,0, G (t, 0));

... (3) G (t, y) = h (x, y -1, G (t, y -1)).

Можна розглядати (3) як систему рiвнянь вiдносно t. Згiдно із (3) для всiх и Î{0,..., у- 1} виконується G (t, u +1) = h (x, и, G (t, и)), тому y = m _u (y = u)або G (t, u +1)¹ h (x, и, G (t, и)). Отже, (3) рiвносильне системі

G (t, 0) = g (x);

y = m _u (| y - u | × nsg (| G (t, u +1)- h (x, и, G (t, и))|)=0). (4)

Позначимо m _u (| y - u | × nsg (| G (t, u +1)- h (x, и, G (t, и))|)=0) як F (x, y, t). Тодi система (4) рiвносильна рiвнянню | G (t, 0)- g (x)| + | y - F (x, y, t)| = 0.

За основною властивiстю функцiї Геделя система (3), отже, i рiвносильне їй рiвняння | G (t, 0)- g (x)| + | y - F (x, y, t)| = 0 має розв'язок вiдносно t для всiх значень x та y, тому iснує мiнiмальний розв’язок t = m _z (| G (z, 0)- g (x)|+| y - F (x, y, z)|=0).

Позначивши таке t як j(x, y), маємо f (x, y) = G (t, y) = G (j(x, y), y).

Функцiя j отримана iз функцiй g, h та функцiй G, +, ´, 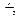nsg i базових функцiй о, s, I за допомогою операцiй S ^{n+ 1}та M. Функцiя G отримується iз функцiй о, s, I і функцiй +, ´, 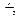mod, l, r за допомогою операцiй S ^{n+ 1}та M. У свою чергу, функцiї l і r отриманi iз функцiй 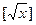, [ x /2], о, s, I , +, ´ 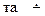за допомогою операцiй S ^{n+ 1}. Функцiї 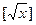, [ x /2] і mod можуть бути отриманi iз функцiй о, s, I , +, ´ 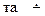за допомогою операцiй S ^{n+ 1}і М. Але nsg (x)= 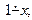тому функцiя G отримується iз функцiй о, s, I , +, ´ 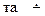за допомогою операцiй S ^{n+ 1}і М. Отже, функцiя j, а тому i функцiя f одержуються iз функцiй g, h, о, s, I , +, ´ 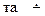за допомогою операцiй суперпозицiї S ^{n+ 1}та мiнiмiзацiї М.

Наслiдок. Клас ЧРФ збігається з класом функцiй, отриманих iз функцiй о, s, I , +, ´ 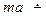за допомогою скiнченної кiлькостi застосувань операцiй S ^{n+ 1} і M.

ЛЕКЦІЯ 7

ПЛАН

1. Еквівалентність формальних моделей алгоритмів.

2. Теза Чорча, її обгрунтування. Значення тези Чорча та її використання.

Поиск по сайту: