 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Машини Тьюрінга. Обчислюваність за Тьюрінгом
Пiд (детермінованою) машиною Тьюрiнга (скорочено МТ) будемо розумiти впорядковану 5-ку (Q,T,d, q0,q*), де:
- Q - скiнченна множина внутрiшнiх станiв;
- T - скiнченний алфавiт символiв стрiчки, причому T мiстить спецiальний символ порожньої клiтки l;
- d: Q ´ T → Q ´ T ´{ R,L,e } - однозначна функцiя переходiв;
- q0 Î Q - початковий стан;
- q* Î Q - фiнальний стан.
Функцiю переходiв на практицi задають скiнченною множиною команд одного з 3-х видiв: qa®pbR, qa®pbL та qa®pb, де p, qÎQ, a, bÎT, ® Ï Q È T. При цьому, як правило, не для всiх пар (q,a)Î Q ´ T iснує команда з лiвою частиною qa. Це означає, що функцiя d не є тотальною. Проте зручніше вважати функцію d тотальною, тому для всiх пар (q,a)Ï Dd неявно (не додаючи вiдповiднi команди вигляду qa®qa) вводимо довизначення d (q,a) = (q,a,e).
Неформально МТ складається зі скiнченної пам’ятi, роздiленої на клiтки нескiнченної з обох бокiв стрiчки та головки читання-запису. В кожнiй клiтцi стрiчки мiститься єдиний символ iз T, причому в кожен даний момент стрiчка мiстить скiнченну кiлькiсть символiв, вiдмiнних вiд символа l. Головка читання-запису в кожен даний момент оглядає єдину клiтку стрiчки.
Якщо МТ знаходиться в станi q та головка читає символ a, то при виконаннi команди qa®pbR (команди qa®pbL, команди qa®pb) МТ переходить у стан p, замiсть символу a записує на стрiчцi символ b та змiщує головку на 1 клiтку направо (відповідно на 1 клiтку налiво, залишає головку на мiсцi).
Конфiгурацiя, або повний стан МТ, - це слово вигляду xqy, де x,yÎT*, q Î Q. Неформально це означає, що на стрiчцi записане слово xy, тобто злiва i справа вiд xy можуть стояти тiльки символи l, МТ знаходиться в станi q, головка читає 1-ий символ пiдслова y.
Конфiгурацiю вигляду q0x, де 1-й та останнiй символи слова x вiдмiннi вiд l, називають початковою. Конфiгурацiю вигляду xq*y називають фiнальною. Пiсля переходу до фiнального стану, отже, до фiнальної конфiгурацiї МТ спиняється.
Нехай МТ знаходиться в конфiгурацiї xcqay, де x,y Î T*, a, c Î T, q Î Q. Пiсля виконання команди qa®pbR (команди qa®pbL, команди qa®pb) МТ перейде до конфiгурацiї xcbpy (вiдповiдно до конфiгурацiї xpcby, конфiгурацiї xcpby).
Кожна МТ задає вербальне вiдображення T* → T* таким чином.
МТ М переводить слово uÎT у слово vÎT*, якщо вона з початкової конфiгурацiї q0u переходить до фiнальної конфiгурацiї xqy, де q Î F*, xy= a v b, a, bÎ{ l } *. При цьому перший та останнiй символи слова v вiдмiннi вiд l, або v=e. Цей факт записуємо так: v=M (u).
Якщо МТ M, починаючи роботу з початкової конфiгурацiї q0u, нiколи не спиниться, кажуть, що M зациклюється при роботi над словом u. Тодi M (u)не визначене.
МТ M1 та M2 еквiвалентнi, якщо вони задають одне і те ж вербальне вiдображення.
МТ M обчислює часткову функцiю f:Nk → N, якщо вона кожне слово вигляду 
переводить у слово 
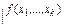у випадку (x 1 ,...,xk)Î Df , та M () не визначене при (x 1 ,...,xk)Ï Df .
Функцiя називається обчислюваною за Тьюрiнгом, або МТ-обчислюваною, якщо iснує МТ, яка її обчислює.
Зауважимо, що кожна МТ обчислює безліч функцій натуральних аргументів та значень, але, зафіксовуючи наперед арність функцій, дістаємо, що кожна МТ обчислює єдину функцію заданої арності.
Розглянемо приклади МT.
Приклад 1. МТ, яка обчислює функцiю x+y:
q0 | ® q 0| R
q 0# ® q 0| R
q 0 l® q 1 lL
q 1| ® q*l
Приклад 2. МТ, яка обчислює функцiю f (x)=sg(x):
q0l® q*l
q 0 |® q 1| R
q 1| ® q 1 lR
q 1 l® q*l
Приклад 3. МТ, яка обчислює функцiю f (x, y) = x - y:
q0 | ® q 1 lR
q 1 |® q 1| R
q 1# ® q 1# R
q 1 l® q 2 lL
q 2 |® q 3 lL
q 3 |® q 3| L
q 3# ® q 3# L
q 3 l® q0lR
q 2# ® q*|
q0 # ® q 4 lR
q 4 l® q*l
Приклад 4. МТ, яка обчислює функцiю f (x, y)= 
q0 | ® q 1 lR
q 1 |® q 1| R
q 1# ® q 1# R
q 1 l® q 2 lL
q 2 |® q 3 lL
q 3 |® q 3| L
q 3# ® q 3# L
q 3 l® q0lR
q 2# ® q*|
q0 # ® q 4 lR
q 4 |® q 4 lR
(єдина відмінність від МТ для f (x, y) = x - y)
q 4 l® q*l
Поиск по сайту: