Властивості ПРМ, РМ і РПМ

Тeорeма 11. Клас РПМ замкнений вiдносно операцiй È та Ç.

Нехай A і B - РПМ, нехай f та g - РФ такi, що A = E_f і B = E_g . Задамо функцiю h так: h (2× x)= f (x), h (2× x +1)= g (x). Тодi h є РФ, причому E_h = E_f È E_g = A È B. Тому A È B є РПМ. Але × , тому - ЧРФ, звідки за df4 A Ç B є РПМ.

Тeорeма 12 (узагальнена тeорeма Поста). Нехай множини A та B - РПМ, причому A Ç B =Æ і множина A È B рекурсивна. Тодi A та B - рекурсивнi множини.

Вважаємо, що A ¹Æ та B ¹Æ, iнакше твердження теореми тривiальне. Нехай f і g - такi РФ, що A = E_f та B = E_g . Вкажемо алгоритм A, який за довiльним b Î N визначає: b Î A чи b Ï A.

Функцiю h (x) задамо так: h (2× x)= f (x), h (2× x +1)= g (x). Тодi h є РФ, причому E_h = E_f È E_g = A È B. Множина A È B рекурсивна, тому алгоритмiчно розв’язна. Спочатку наш алгоритм A моделює роботу алгоритму для розв’язування множини A È B. Якщо b Ï A È B, то b Ï A. Якщо bÎA È B, то поступово обчислюємо значення h (0), h (1),.... Позаяк E_h = A È B, то b = h(n) для деякого n. Якщо п парне, то b = h (n)= f (n /2), звiдки маємо bÎA. Якщо п непарне, то b = h (n)= g ((n -1)/2), звiдки b Î B, тому в силу A Ç B =Æ маємо b Ï A. Отже, множина A алгоритмiчно розв’язна. За тезою Чорча множина A рекурсивна.

Аналогiчно доводимо рекурсивнiсть множини B.

Наслiдок (тeорeма Поста). Якщо множини L та рекурсивно перелiчнi, то множини L і рекурсивнi.

Тeорeма 13. Для довiльних РПМ A та B iснують РПМ L і M такi, що L Í A, M Í B, L Ç M =Æ та L È M = A È B.

Вважаємо A ¹Æ, B ¹Æ і A ¹ B (iнакше твердження теореми є тривiальним). Вiзьмемо a Î A та b Î B такi, що a ¹ b. Нехай f і g - такi РФ, що A = E_f та B = E_g. Задамо функцiї f і y так:

f(0) =

y(0) =

f(x+ 1) =

y(x+ 1) =

За ТЧ f та y є РФ. Тодi множини L = E _f та M = E _y задовольняють умову теореми.

Для довiльної L Í N уведемо позначення

L _2x ={2 x | x Î L } та L _{2х + 1} ={2 x +1| xÎL }.

Для множин, заданих на N, визначимо операцiї сполучення Å та добутку Ä:

A Å B = {2 x | x Î A }È{2 x +1| x Î B }= A _2xÈ B _2x+1;

A Ä B = { C (x, y)| x Î A, y Î B }.

Тeорeма 14. 1) Множини A та B РМ/РПМ Û A Å B РМ/РПМ.

2) Якщо A ¹Æ і B ¹Æ, то A та B РМ/РПМ Û A Ä B РМ/РПМ.

Доведемо для випадку РПМ. Для випадку РМ доведення аналогiчне, тiльки замiсть часткових характеристичних функцiй беремо характеристичнi функцiї вiдповiдних множин.

Маємо x Î A Å B Û (x парне та x /2Î A) або (x непарне і (x -1)/2Î B).

Якщо A та B є РПМ, то є ЧРФ за ТЧ, тому A Å B є РПМ.

Маємо x Î A Û 2 x Î A Å B і x Î B Û 2 x +1Î A Å B. Звiдси = , = . Тому якщо A Å B є РПМ, то A та B теж є РПМ.

Маємо x Î A Ä B Û l (x)Î A і r (x)Î B, звiдки дiстаємо = 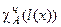× . Тому якщо A та B є РПМ, то A Ä B є РПМ.

Зафiксуємо довiльнi a Î A, b Î B. Маємо

x Î A Û C (x, b)Î A Ä B, x Î B Û C (а, х)Î A Ä B.

Тому = , = . Якщо A Å B є РПМ, то множини A та B теж є РПМ.

Ефективну нумерацiю РПМ уведемо на основi нумерацiй n -арних ЧРФ згiдно з df3:

номером (iндексом) РПМ L Í Nⁿ є номер n-арної ЧРФ f такої, що L = D_f.

РПМ L Í Nⁿ з iндексом m позначатимемо 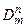, або D_m для випадку n =1.

Множину { L Í Nⁿ | L є РПМ} будемо позначати РПМ ^п. Аналогiчно вводимо позначення РМ ^п та ПРМ ^п.

ЛЕКЦІЯ 12

ПЛАН

1. Поняття примітивно рекурсивного, рекурсивного та частково рекурсивного предиката (ПРП, РП і ЧРП).

2. Властивості ПРП, РП та ЧРП.

1. Поняття примітивно рекурсивного, рекурсивного і частково рекурсивного предиката (ПРП, РП та ЧРП)

n -арний предикат на N називають рекурсивним (скорочено РП), якщо його характеристична функцiя рекурсивна.

n -арний предикат на N називають примiтивно рекурсивним (скорочено ПРП), якщо його характеристична функцiя є ПРФ.

Безпосередньо iз визначень випливає, що кожний ПРП є рекурсивним предикатом.

n -арний предикат на N називають частково рекурсивним (скорочено ЧРП), якщо його часткова характеристична функцiя є ЧРФ.

Замiсть " P (x ₁,..., x_n)= Т " надалі будемо також писати " P (x ₁,..., x_n)".

Поиск по сайту: