Властивості ймовірності

1. Ймовірність достовірної події дорівнює одиниці.

У цьому випадку т = п, відповідно .

2. Ймовірність неможливої події дорівнює нулю.

У цьому випадку т= 0, відповідно Р(Æ)= .

3. Ймовірність випадкової події АÌ 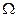є додатнє число, що лежить у межах від нуля до одиниці, тобто 0≤ ≤1

Задача 10. В урні 15 білих і 10 чорних куль. З урни навмання виймають три кульки. Знайти ймовірність того, що

1) всі три кульки білі (подія А);

2) дві кулі білі і одна чорна (подія В).

Розв’язання. Випробування – поява з урни, що містить 25 кульок, трьох кульок.

1) Число всіх елементарних подій дорівнює числу комбінацій з 25 по 3, тобто 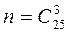. Знаходимо число сприятливих випадків для події А. Три білі кульки можна вибрати з 15 білих кульок 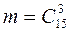способами. Отже, шукана ймовірність дорівнює

.

2) Аналогічно до пункту 1), . Знайдемо число сприятливих випадків. Дві білі кульки можна вибрати з 15 білих кульок способами, а одну чорну з десяти чорних – способами. За правилом множення одержимо т=k₂·k₁ = 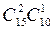. Тому маємо .

Відповідь: 1) 0,2; 2) 0,46.

Поиск по сайту: