Рівень Б. 1. На малюнку зображено графік

1. На малюнку зображено графік

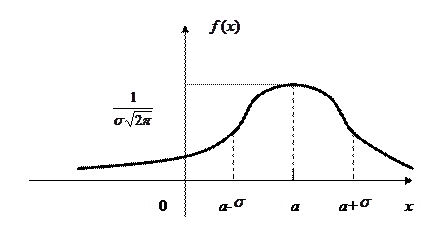
1) нормального закону розподілу;

2) показникового закону розподілу;

3) рівномірного закону розподілу.

2. Випадкову величину Х називають розподіленою нормально, якщо щільність її ймовірностей має вигляд

1) ;

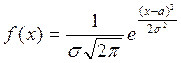2) ;

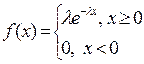3) .

3. Оберіть неправильне твердження:

1) Математичне сподівання сталої величини є сама ця стала М(С)=С.

2) Сталий множник можна виносити за знак математичного сподівання М(СХ)=СМ(Х).

3) Математичне сподівання суми двох випадкових величин дорівнює добутку їх математичних сподівань.

4. Оберіть правильне твердження:

1) D(C)=0, C – стала величина;

2) сталий множник можна винести за знак дисперсії;

3) дисперсія різниці незалежних випадкових величин дорівнює різниці їх дисперсій.

5. Розподілом дискретної випадкової величини є

1) рівномірний розподіл;

2) показниковий;

3) біноміальний.

6. Математичне сподівання НВВ, розподіленої за біноміальним законом розподілу, знаходять за формулою:

1) np;

2) npq

3)

7.Для будь-якої випадкової величини Х ймовірність того, що вона відхиляється від свого математичного сподівання більше, ніж на число 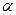, завжди менша, ніж

1) ;

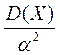2) ;

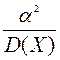3) .

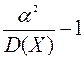8. Ймовірність настання принаймні однієї з подій А₁, А₂,..., А_п , незалежних в сукупності, знаходиться за формулою:

1) ;

2) ;

3) .

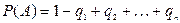9. Чи справедлива рівність 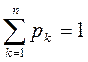, де р_к – ймовірність значень ДВВ,

1) так;

2) ні.

10. Аналітичний вираз , де 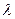>0, п =0,1,2,...має назву

1) формула Пуассона;

2) локальна теорема Муавра – Лапласа;

3) інтегральна теорема Муавра – Лапласа.

Поиск по сайту: