Сполуки з повторенням елементів

Означення. Розміщеннями з повтореннями із n елементів по k називається будь-яка упорядкована сполука, що містить k елементів, взятих ізданих n елементів серед яких є однакові.

Число всіх розміщень із повтореннями по k позначається і обчислюється за формулою = n^k.

Приклад. Нехай маємо множину А={а, b, с}, тоді розміщення з повторенням по два елементи – це пари (а, а), (а, b), (а, с), (b, b), (b, с), (b, а), (с, с), (с, а), (с, b). Їх кількість дорівнює 9, або .

Задача 4. Скількома способами можна розмістити 5 файлів різного формату у 3 папки?

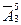Розв’язання. Шукана кількість способів обчислюється за формулою = n^k. У даному випадку. =3⁵=243.

Відповідь: 243 способа.

Означення. Перестановкою з повторенням із n елементів називається будь-яке впорядкування множини з п елементів, серед яких є однакові.

Якщо серед п елементів множини є п₁ першого типу, п₂ другого типу,..., п_к елементів к –того типу (п₁+п₂ +...+ п_к=п), то число всіх перестановок такої множини позначається і обчислюється за формулою

.

Задача 5. Скільки різних слів (беззмістовних) можна утворити перестановкою букв у слові „головоломка”?

Розв’язання. Слово „головоломка” містить 11 букв, серед них буква „о” зустрічається 4 рази, „л” – 2 рази, всі інші по одному разу.

За формулою 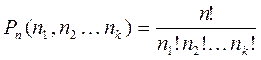, маємо

.

Відповідь: 34650 слів.

Означення. Сполученнями з повтореннями із п елементів по к називається сполука, що містить к елементів взятих з даних п елементів серед яких є однакові.

Число всіх комбінацій з повтореннями із п елементів по к позначається і обчислюється за формулою = .

Задача 6. Скількома способами можна роздати десять однакових цукерок трьом дітям?

Розв’язання. Шукане число способів дорівнює .

Відповідь: 66 способів.

Поиск по сайту: