АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Граничні теореми у схемі Бернуллі

Читайте также:
  1. Граничні блага і громадський вибір
  2. Граничні витрати та граничний дохід
  3. Граничні теореми теорії ймовірності
  4. Задачі на теореми складання і множення ймовірностей
  5. Лекція 41: Повторні незалежні випробування. Формула Бернуллі. Статистичне визначення ймовірності.
  6. Наймовірніше число успіхів у схемі Бернуллі
  7. Основні теореми і формули
  8. Рекурентна форма математичної моделі руху судна (за методом кінцевих різниць) та сформувати початкові та граничні умови.
  9. Рівносильні рівняння. Теореми про рівносильність рівнянь.
  10. Теореми додавання і множення
  11. Теореми додавання ймовірностей

 

Знаходження ймовірності за схемою Бернуллі ускладнюється, якщо п дуже велике і р або q дуже малі числа.

Для такого випадку застосовують наближені формули:

а) формула Пуассона

Справедлива наближена рівність

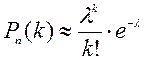, де , (8)

Ця формула дає досить точне наближення при та р близьких до нуля (р <0,1), тобто для подій, які рідко трапляються.

Задача. 19. Середній брак при виробництві продукції становить 0,1%. Перевіряється партія з 1000 деталей. Яка ймовірність того, що бракованих буде 4 деталей?

Розв’язання. З а умовою задачі n =1000, p =0,001→0, λ= np =1000*0,001=1. При таких умовах застосовуємо формулу Пуассона: . Отже, маємо .

Відповідь: 0,0153.

б) локальна теорема Муавра-Лапласа

Справедлива наближена рівність

, (9)

де , – локальна функція Муавра-Лапласа.

Функція парна. Таблиця значень функції наведена у додатку 2. Формула (9) дає добре наближення, якщо п достатньо велике, а 0<р<1.

Задача 20. При виробництві деякої продукції ймовірність виготовлення 1-го сорту приймається рівною 0,60. Визначити ймовірність того, що із 100 навмання взятих виробів 65 будуть першого сорту.

Розв’язання Нехай подія А – виготовлення виробу першого сорту. За умовою n =100, k =65, p =0,60, q =0,40. Оскільки n достатньо велике число, p не прямує ні до 0, ні до 1, то скористаємося локальною теоремою Муавра-Лапласа: .

.

За таблицею значень локальної функції Лапласа (додаток 2) знаходимо, що . Тому шукана ймовірність

.

Відповідь: 0,045.

в) інтегральна теорема Муавра-Лапласа

Ймовірність того, що при п незалежних випробуваннях, в кожному з яких подія А може відбутися з ймовірністю р (0< р <1), подія А відбудеться не менше к1 і не більше к 2 разів, наближено дорівнює

(10)

де – інтегральна функція Муавра-Лапласа.

Функція непарна. Таблиця значень інтегральної функції наведена у додатку 3. Для всіх значень х≥5 можна вважати .

Задача 21. Ймовірність виходу з ладу одного приладу дорівнює 0,1. Визначити ймовірність того, що за час Т зі 100 приладів вийде з ладу від 6 до 18 приладів.

Розв’язання З а умовою задачі n =100, k1 =6, k2 =18, p =0,1, q =1‑ p =1‑0,1=0,9. Скористаємося інтегральною теоремою Муавра-Лапласа: .

.

За таблицею значень інтегральної функції Лапласа (додаток 3) знаходимо:

Ф(2,66)=0,4961, Ф(-1,33)=-Ф(1,33)=-0,4082.

Тому .

Відповідь: 0,9043.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)