АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Наймовірніше число успіхів у схемі Бернуллі

Читайте также:
  1. Ni – число абонентских номеров для i- ой ТС.
  2. Атомная масса и атомное число.
  3. АУТОДАФЕ И ЧИСЛО ЖЕРТВ
  4. В журнале движения больных отделения отмечаются сведения о движении больных: число выбывших и поступивших.
  5. Випадкові події і величини, їх числові характеристики
  6. Вопрос 1 Числовые характеристики случайных величин.
  7. Вопрос 1 Числовые характеристики статистического распределения
  8. Где i - величина равного интервала; Хmax, Хmin - наибольшее и наименьшее значения признака; n - число групп.
  9. Где n - число групп; N - число единиц совокупности.
  10. Гелий и гелион. Массовое число атома. Атомное число.
  11. Граничні теореми у схемі Бернуллі
  12. Двовимірний статистичний розподіл вибірки та його числові характеристики.

Означення 1. Найімовірнішим числом m0 появи події А в n незалежних випробовуваннях називається число, для якого ймовірність не менша ймовірності кожного з решти можливих варіантів, тобто

.

Якщо найімовірніше число , то повинні виконуватись такі умови:

. (1)

. (2)

З нерівності (1) отримується:

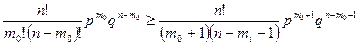
звідки (після скорочень)

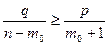
Розв’язуючи нерівність відносно , отримують:

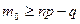. (3)

Аналогічно з нерівності (2) отримується:

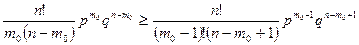
Звідки

; . (4)

Остаточно отримується нерівність:

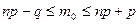. (5)

Зауваження. Довжина інтервалу, що визначається нерівністю (5), рівна одиниці:

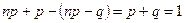
тому, коли межі інтервалів є дробові числа, то отримується одне значення наймовірнішого числа , якщо ж межі є цілими числами, то отримується два значення наймовірнішого числа успіхів

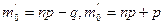
Приклад 1. При даному технологіному процесі 90% всієї продукції – вищого сорту. Знайти наймовірніше число виробів вищого сорту в партії з 200 виробів.

Рішення. За умовою n=200, p=0,9, q=0,1

Тоді ,

.

Отже .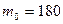

Приклад 2. Гральний кубик кидають 35 раз. Яке найвірогідніше число випадання грані з одиницею?

Рішення. В цьому прикладі n=35, p= ,q= , тому

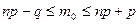, де ,

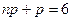
Тому - найвірогідніших значень два.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)