Ймовірність об’єднання сумісних подій

Теорема 3. Ймовірність об’єднання двох сумісних подій рівна сумі ймовірностей цих подій мінус ймовірність їх перетину:

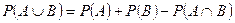. (7)

Доведення. Щоб відбулася подія А потрібно, щоб відбулася хоча б одна з несумісних подій А 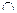В або А . Аналогічно, щоб відбулася подія В

досить, щоб відбулася хоча б одна з несумісних подій:

А або .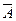

Тому на основі теореми додавання ймовірностей для несумісних подій маємо

, (8)

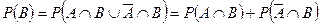. (9)

Для того, щоб відбулася хоча б одна з подій А та В, досить, щоб відбулася хоча б одна з несумісних подій . Тому

. (10)

Додавши рівності (8), (9), знайдем:

Підставивши цей вираз в (10), отримаєм:

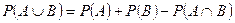
Теорема доведена.

Формулу (7) можна узагальнити на випадок довільного скінченного числа подій (див. аналогічно Розд.1,§1, формула (4)).

+

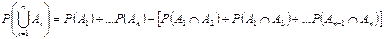+ (11)

Практично використовувати формулу (11) є громіздко, тому краще перейти до протилежної події, а саме:

. (12)

Приклад 1. Виконується два постріли по мішені. Ймовірність попасти при першому пострілі 0.7, для другого – 0.8. Знайти ймовірність того, що буде хоча б одне попадання.

Рішення. Нехай, подія А₁ – попадання при першому пострілі; А₂ – попадання при другому пострілі; А – хоча б одне попадання. Тому А=А₁ 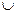А₂, причому А₁, А₂ – події сумісні та незалежні. Згідно з формулами (7), (6), отримаємо:

= .

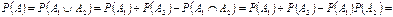
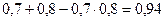Приклад 2. Робітник обслуговує чотири верстати, які працюють незалежно один від одного. Ймовірність того, що протягом години перший верстат не потребує обслуговування робітника, рівна 0.92, для другого – 0.9, для третього – 0.85, для четвертого – 0.8. Яка ймовірність того, що протягом години хоча б один верстат не потребуватиме обслуговування робітника?

Рішення. Позначимо А_і (і= 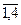) подію “і-ий верстат протягом години не потребує обслуговування”, через А – “протягом години хоча б один верстат не потребує обслуговування ”. Тоді А=А_{1 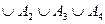.} Події А_і (і= 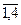) сумісні та незалежні, тому можна використати формулу (11), а краще використаємо формулу (12):

,

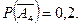
тобто подія А практично майже достовірна.

Поиск по сайту: