АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Рівномірний закон розподілу задається густиною розподілу

Читайте также:
  1. B) Наличное бытие закона
  2. II закон Кирхгофа
  3. II. Законодательные акты Украины
  4. II. Законодательство об охране труда
  5. II.3. Закон как категория публичного права
  6. III. Государственный надзор и контроль за соблюдением законодательства об охране труда
  7. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  8. IX.3.Закономерности развития науки.
  9. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  10. А 55. ЗАКОНОМІРНОСТІ ДІЇ КОЛОГИЧЕСКИХ ФАКТОРІВ НА ЖИВІ ОРГАНІЗМИ
  11. А) Закон диалектического синтеза
  12. А) совокупность предусмотренных законодательством видов и ставок налога, принципов, форм и методов их установления.

, (10)

де С = const (див. лк.24, §1).

Тому запишемо

,

Знайдемо інтегральну функцію розподілу F(x), яка буде:

.

тобто

,

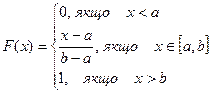а її графік буде

 
 

 

 


Знайдемо числові характеристики розподілу:

 

а) математичне сподівання:

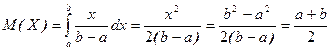
б) дисперсія:

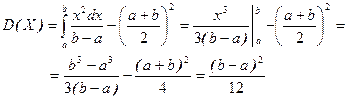
в) середнє квадратичне відхилення:

.

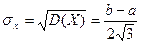Показниковий (експоненціальний) розподіл, коли випадкова величина має густину розподілу у вигляді:

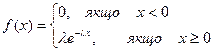(11)

де l - параметр розподілу.

Випадкова величина Х з таким законом розподілу часто зустрічається в прикладних питаннях теорії ймовірності, особливо в теорії масового обслуговування.

Знайдемо інтегральну функцію розподілу:

,

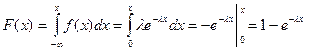тобто

.

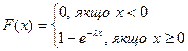Наведемо графіки функцій 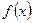і :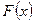

 
 

 

 


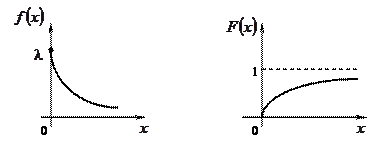Знайдемо числові характеристики показникового розподілу:

а) математичне сподівання;

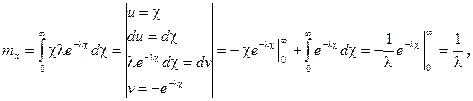тобто ;

б) дисперсія:

в) середнє квадратичне відхилення:

.

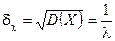Отже, .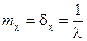

Приклад 1. Випадкова величина Т – час роботи елементу – має показниковий розподіл. Знайти ймовірність того, що час роботи елементу буде не менше 600 годин, якщо середній час роботи елементу 400 годин.

Рішення. За умовою математичне сподівання (середній час роботи елементу) 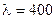, значить:

.


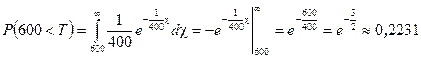1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)