 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Граничні теореми теорії ймовірності
1. Локальна теорема Муавра-Лапласа
Очевидно, що користуватись формулою Бернуллі при великих значеннях n досить важко, бо формула вимагає виконання дій над великими числами. Виникає питання, чи можна обчислити ймовірність, не звертаючись до формули Бернуллі? Можна, застосовуючи локальну теорему Лапласа, що дає асимптотичну (наближену) формулу, яка визначає наближену ймовірність появи події рівно m раз в n випробовуваннях, якщо число випробовувань досить велике.
Теорема 1. (локальна теорема Лапласа). Якщо ймовірність р появи події А в кожному випробовуванні постійна (0<p<1), то ймовірність 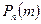 того, що подія А відбудеться в
того, що подія А відбудеться в  випробовуваннях рівно
випробовуваннях рівно 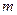 раз, наближено рівна (тим точніше, чим більше
раз, наближено рівна (тим точніше, чим більше  ) значенню функції
) значенню функції
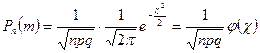
при 
Функція Лапласа  табульована, причому таблиці складені лише для додатніх значень аргументу, оскільки функція
табульована, причому таблиці складені лише для додатніх значень аргументу, оскільки функція 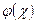
парна  (див. табл. 1).
(див. табл. 1).
Приклад 1. Знайти ймовірність того, що подія А відбудеться 90 раз в 400 випробовуваннях, якщо ймовірність появи цієї події в кожному випробовуванні рівна р=0.2.
Рішення. За умовою 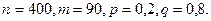
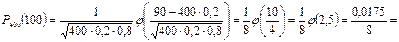
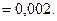
Поиск по сайту: