Функція надійності

Нехай деякий елемент починає працювати в момент часу , а після деякого проміжку часу відбувається збій. Якщо позначити через неперервну випадкову величину – час безвідмовної роботи елементу, то якщо елемент пропрацював безвідмовно час, менший , то значить, за час наступить збій.

Таким чином, функція розподілу 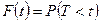визначає ймовірність відмови елементу за час . Значить, ймовірність безвідмовної роботи за цей самий час , тобто ймовірність протилежної події , рівна

. (1)

Означення. Функцією надійності називається функція, що визначає ймовірність безвідмовної роботи елементу за час .

.

Часто час безвідмовної роботи елементу має показниковий розподіл, функція розподілу якого є 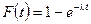, тобто функція надійності

.

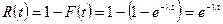Показниковим законом надійності називається функція:

, (2)

де - інтенсивність відмовлень.

Приклад 1. Час безвідмовної роботи елементу розподілений за показниковим законом . Знайти ймовірність

того, що елемент пропрацює безвідмовно 50 год.

Рішення. Інтенсивність відмовності . Тоді .

Лекція 6. ЗАКОН ВЕЛИКИХ ЧИСЕЛ

Теорія ймовірностей вивчає закономірності, що властиві масовим випадковим явищам. Як і всяка інша наука, теорія ймовірності створена для того, щоб по можливості найбільш точно передбачити результат того чи іншого явища, події. Проте, якщо це явище носить одиничний, не масовий характер, то теорія ймовірностей здатна передбачити ймовірність результату в досить широких межах. Зовсім інша справа, коли явище – масове. Закономірності проявляються саме при великому числі випадкових явищ, що відбуваються в однорідних умовах. При досить великому числі випробувань характеристики випадкових величин, що спостерігаються при випробуваннях стають майже невипадковими. Так, наприклад, частота події при великому числі випробувань стає стійкою, те ж саме відноситься до середнього значення випадкової величини. Цей факт дозволяє використати результати спостережень над випадковими явищами для передбачення результатів майбутніх випробувань.

Група теорем, що встановлює відповідність між теоретичними і експериментальними характеристиками випадкових величин і випадкових подій при великому числі випробувань над ними, а також зв’язаних з ними граничних законів розподілу, об’єднується під загальною назвою граничних теорем теорії ймовірності.

В даному розділі ми познайомимося з двома типами граничних теорем:

Поиск по сайту: