Диференціальна функція розподілу

Виникає питання: яким чином, спостерігаючи випадкові значення Х, побудувати функцію розподілу 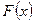. Виявляється, що до цієї функції практично простіше підходити через іншу функцію.

Нехай 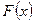- неперервна і диференційована функція розподілу випадкової величини Х. Підрахуємо ймовірність попадання значень на інтервал 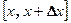, а саме:

.

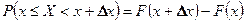Поділимо цю рівність на 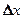і перейдемо до границі при умові :

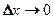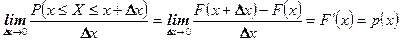(3)

Отримана похідна 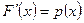називається густиною (щільністю) розподілу випадкової величини Х, або диференціальною функцією розподілу. В літературі часто її позначають . Зміст густини розподілу полягає в тому, що вона вказує, як часто появляється випадкова величина Х в деякому околі точки х при повторенні випробувань.

Властивості густини розподілу:

Властивість 1. Густина розподілу невід’ємна, тобто .

Дійсно, бо 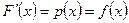, а 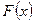- неспадна функція.

Властивість 2. Функція розподілу випадкової величини рівна

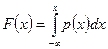, (4)

Дійсно, , тобто .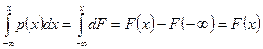

Властивість 3. Ймовірність попадання неперервної випадкової величини на інтервал 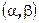рівна

.

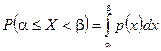Дійсно , , .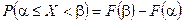

Тому

.

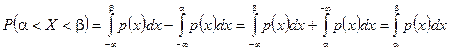Властивість 4. .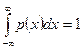

Дійсно

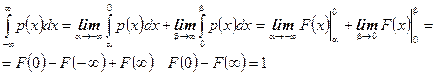
Приклад. Випадкова величина Х розподілена рівномірно на відрізку 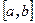, тобто вона має густину розподілу такого вигляду:

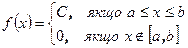
Знайдемо постійну С:

.

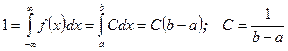Отже,

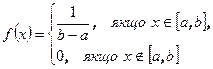
з її графіком (рис.1).

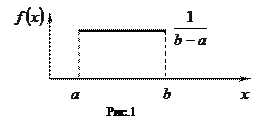Якщо відрізок 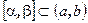, то ймовірність попадання випадкової величини Х в рівна:

.

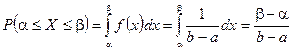Поиск по сайту: