АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Властивості функції розподілу

Читайте также:
  1. III. Соціальна політика, її сутність і функції.
  2. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  3. А) Властивості бінарних відношень
  4. АБСТРАКТНІ КЛАСИ І ЧИСТІ ВІРТУАЛЬНІ ФУНКЦІЇ_________________________________________
  5. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  6. Автоматизоване робоче місце бухгалтера (АРМБ): призначення, функції та його рівні.
  7. Алгоритм знаходження функції, оберненої до даної.
  8. Атрибутивні ознаки і властивості культури
  9. Б) Основні властивості операцій над множинами
  10. Банківська система. Банки, їх види та функції
  11. Банківська система. Банки, їх види та функції
  12. Біноміальний закон розподілу

1. Функція розподілу випадкової величини є невід’ємна функція, заключна між нулем і одиницею .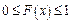

2. Функція розподілу випадкової величини є не спадаюча функція на усій числовій осі.

3. На мінус нескінченності функція розподілу дорівнює нулю, на плюс нескінченності дорівнює одиниці, тт. , .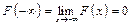

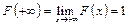4. Ймовірність попадання випадкової величини в інтервал 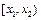дорівнює прирощенню її функції розподілу на цьому інтервалі, тт.

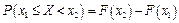(1.30)

Приклад 1.22. Випадкова величина Х задана функцією розподілу ймовірностей

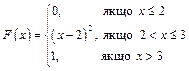
Знайти ймовірність попадання випадкової величини в інтервал (2,5; 3,5).

Розв’язання. Ймовірність попадання випадкової величини 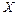в заданий інтервал обчислюємо за формулою (1.30)

.

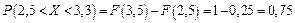Щільністю ймовірності (щільністю розподілу або просто щільністю) 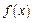неперервної випадкової величини 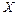називається похідна її функції розподілу

(1.31)

Щільність імовірності іноді називають диференціальною функцією або диференціальним законом розподілу.

Графік щільності ймовірності називають кривою розподілу.

Приклад 1.23. Випадкова величина 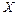задана функцією розподілу

.

Знайти диференціальну функцію.

Розв’язання. Використавши формулу (1.32), отримаємо

.

 


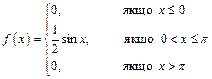1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)