 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Основні закони розподілу
Основні закони розподілу для дискретних і неперервних величин разом з їх числовими характеристиками наведемо в таблицях 1.1 і 1.2.
а) Дискретна випадкова величина
|
| № n/n | Закони розподілу | Обчислення ймовірності

| Числові характеристики | |

| 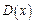
| |||
| Біномний | 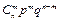 ,
де ,
де 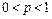 , , 
| 
| 
| |
| Пуассона |  ,
де ,
де 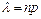
| 
| 
| |
| Геометричний | 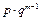
| 
| 
| |
| Гіпергеометричний |  ,
де ,
де
 ; ;
 , ,  ; ;
 – натуральні числа – натуральні числа
|  ,
де ,
де  – сукупність об’єктів; – сукупність об’єктів;
 – кількість об’єктів, які мають такі ж властивості – кількість об’єктів, які мають такі ж властивості
|  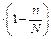
|
|
| № n/n | Закони розподілу | Функція розподілу 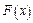
| Щільність ймовірності 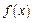
| Числові характеристики | |

| 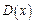
| ||||
| Рівномірний |  ,
де ,
де  і і  – кінці відрізка – кінці відрізка 
| 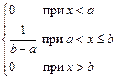
| 
| 
| |
| Показниковий (експоненціальний) |  ,
де ,
де  – параметр експоненти – параметр експоненти
| 
| 
| 
| |
| Нормальний |  ,
де ,
де 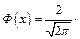  ,
де ,
де  ; ;  – математичне сподівання; – математичне сподівання;
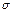 – середнє квадратичне відхилення – середнє квадратичне відхилення
|  
| 
| 
| |
| Логарифмічно- нормальний |   ,
де ,
де  ; ;  – математичне сподівання; – математичне сподівання;
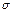 – середнє квадратичне відхилення – середнє квадратичне відхилення
|  
| 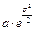
| 

|
Поиск по сайту: