 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Неперервні випадкові величини і їх числові характеристики
Функцією розподілу (інтегральною функцією розподілу або інтегральнимзаконом розподілу) випадкової величини Х називається функція 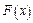 , яка визначає для кожного значення х ймовірність того, що випадкова величина Х набуде значення менші від числа х:
, яка визначає для кожного значення х ймовірність того, що випадкова величина Х набуде значення менші від числа х:
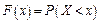 (1.29)
(1.29)
Приклад 1.21. Дано ряд розподілу випадкової величини
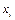
| ||||

| 0,3 | 0,2 | 0,4 | 0,1 |
Х:
Знайти і зобразити графічно її функцію розподілу.
Розв’язання. Будемо задавати різні значення х і знаходити для них 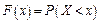
1. Якщо  , то
, то  (в тому числі і при
(в тому числі і при 
 ).
).
2. Нехай  (наприклад, х = 2);
(наприклад, х = 2);  . Очевидно, що й
. Очевидно, що й  .
.
3. Нехай  (наприклад,
(наприклад,  );
);  . Очевидно, що й
. Очевидно, що й  .
.
4. Нехай  .
.  . Очевидно, що й
. Очевидно, що й  .
.
5. Нехай  .
. 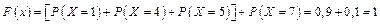
Отже,
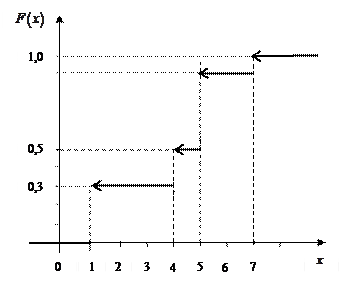
 .
.
Зобразимо функцію 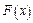
графічно (рис. 5).
Функція розподілу лю-
бої дискретної випадкової ве-
личини є розривна ступенева
функція, стрибки якої прохо-
дять в точках, що відповідають
можливим значенням випадко-
вої величини і рівні ймовірно-
стям цих значень. Сума усіх
|
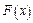 дорівнює
дорівнює
одиниці.
Поиск по сайту: