АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Інтегральна теорема Муавра-Лапласа

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Внешние эффекты (экстерналии). Теорема Коуза.
  3. Внешние эффекты, их виды и последствия. Теорема Коуза
  4. Вопрос 1 теорема сложения вероятностей
  5. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  6. Вопрос. Теорема Котельникова (Найквиста)
  7. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  8. Гранична теорема Пуассона
  9. Дискретизація сигналу – теорема відліків (Котельникова)
  10. Друга теорема економіки добробуту та її значення
  11. Друга теорема розвинення
  12. Заняття 3. Потік вектора напруженості електричного поля. Теорема Гауса

Якщо ймовірність 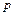появи події 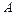в кожному іспиті стала і відмінна від нуля і одиниці, то ймовірність того, що подія 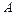з’явиться в 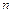іспитах від 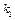до разів, наближено дорівнює

, (1.24)

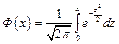де і , .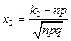

Функція Лапласа Ф() – непарна (Ф(- ))= – Ф(), монотонно зростаюча (при , Ф ) і обчислюється за таблицею додатку 2.

Наближені формули Муавра-Лапласа застосовують практично у випадках коли 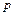і 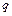не малі а 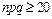[1]. При цій умові формули (1.23) і (1.24) дають незначні похибки обчислення ймовірностей.

Приклад 1.18. В деякій місцевості на кожні 100 сімей припадає 80 холодильників. Знайти ймовірність того, що з 400 сімей: а) 300 сімей мають холодильники; б) від 320 до 350 сімей (включно) мають холодильники.

Розв’язання. Ймовірність того, що сім’я має холодильник 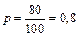. Перевіримо умову застосування формул (1.23) і (1.24.)

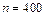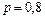, , , тоді .

Отже, теоремами Муавра-Лапласа можна користуватися.

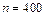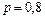а) Скориставшись локальною теоремою Муавра-Лапласа. Спочатку визначимо , враховуючи, що , , , , тоді

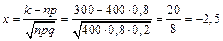
Користуючись додатком 1 позначенню знайдемо 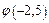, врахувавши парність .

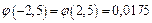Отже, за формулою (1.23) маємо: .

б) За умовою , , , , .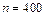

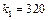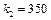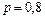Визначимо і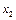

,

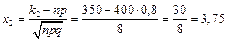
Ф(0)=0, Ф(3,75)=0,499890005-0 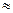0,5

Отже, за формулою (1.24) маємо

.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)