Заняття 3. Потік вектора напруженості електричного поля. Теорема Гауса

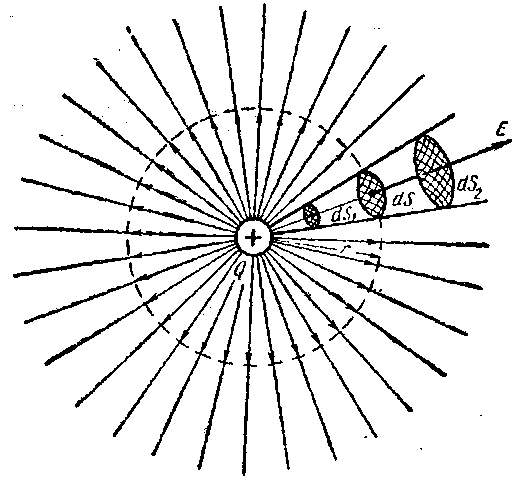Роздивимося електричне поле у формі кулі. Тепер виділимо елемент його поверхні площею d*S. Він являє собою маленьку частину поверхні цієї кулі з радіусом r, у центрі якої є позитивний заряд Q.

У силу геометричної симетрії поля вектор напруженості Е є

однаковим в усіх точках кулястої поверхні і направлений

перпендикулярно до поверхні. Е*d*S виражає

величину елементарного потоку d*N вектора

напруженості електричного поля через елемент

поверхні d*S, якщо лінії напруженості перпендикулярні

до пронизуючої ними поверхні:

d*N= E*d*S.

Визначимо повний потік N вектора напруженості електричного поля,

для чого складемо елементарні потоки по усій поверхні кулі:

N= φ*E*d*S

Винесемо постійне значення Е за знак суми й враховуючи те,що вектор Е повсюди перпендикулярне площі кулі, отримуємо

N=E* φ*d*S,

де φ*d*S= 4πr²- площа поверхні кулі,

N=E*4πr²

Підставимо значення напруженості поля з формули:

N= Q/ε_0.

Приведені міркування вірні і при від’ємному заряді, з той різницею що потік вектора напруження в цьому випадку від’ємний.

З формули слідує, що потік N не залежить від радіусу кульової поверхні.

Потік вектора напруження електричного поля можна придати деяку наочність за допомогою ліній напруження.

Внаслідок симетрії електричного поля в розглянутому випадку лінії напруження називають всю поверхню кулі, і їх щільність(число ліній на одиницю поверхні) однакова. Припустимо, що ця щільність вибрана чисельно рівною напруженості поля. Тоді загальне число ліній, пронизуючих кульову поверхню, буде чисельно рівною повному потоку вектора напруження поля N.

Число ліній напруження, отже, і потоку вектора напруження залишаються однаковими для сфери любого радіуса. Це справедливо і для елементів dS₁ і dS₂ кульових поверхонь, через котрі проходять одні і ті ж лінії напруженості

Елементарний потік вектора

напруженості врахований в

середині конуса, основою якого

являється вибраний елемент поверхні, а

вершина знаходиться в центрі кулі.

Лінії напруженості електричного поля,

враховані в середині вказаного конуса і пронизуючи елемент поверхні dS, створюють елементарну трубку поля. Склавши потоки всіх трубок по всьому об’єму кулі, отримаємо повний потік вектора напруженості електричного поля точкового зарядженого тіла.

Можна довести, що формула справедлива не тільки для сфери, оточуючого точкового зарядженого тіла, але і для будь якої замкнутої поверхні.

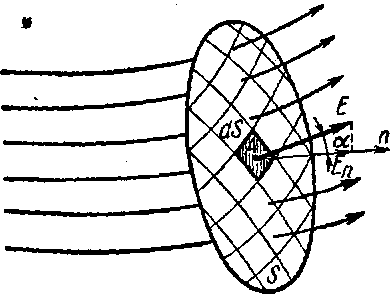
В загальному випадку направлення вектора напруженості Е, може бути не перпендикулярно до елемента поверхні dS близько вибраної точки А

Кут між направленим вектором Е і зовнішньою нормаллю n до поверхні в точці А позначимо α.(Зовнішня нормаль – це лінія, перпендикулярна до поверхні в вибраній точці, направленої від цієї поверхні з зовнішньої сторони.) Для знаходження потоку через елемент поверхні потрібно взяти проекцію вектора Е на направлення зовнішньої нормалі:

dN= E_n dS,

де

E_n=E cosα.

Тоді

dN= E cosα dS.

Додавання елементарних потоків по всій замкнутій поверхні дає повний потік:

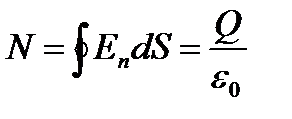, (1.7)

Якщо в середині замкнутої поверхні знаходиться будь яке число тіл з різнойменними зарядами, в формулах(1.6) і (1.7) слідує ввести алгебраїчну суму всіх зарядів:

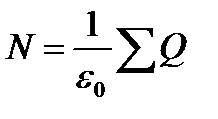(1.8)

Алгебраїчна сума зарядів береться в даному випадку тому, що лінії напруженості при позитивних і негативних зарядах направлені протилежно.

Формула(1.8) являється математичним виразом теореми Гауса, яка формулюється так: потік вектора напруженості електричного поля крізь замкнуту поверхню в порожнечі рівно відношенню електричного заряду, укладеного в середині цієї поверхні, до електричної сталої.

Поиск по сайту: