АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Формули Бейеса дозволяють переоцінювати ймовірності гіпотез після того, як становиться відомим результат випробування, в якому з’являється подія А

Читайте также:
  1. A)нахождение средней из двух соседних средних, для отнесения полученного результата к определенной дате
  2. III. Анализ результатов психологического анализа 1 и 2 периодов деятельности привел к следующему пониманию обобщенной структуры состояния психологической готовности.
  3. III. Принципы конечного результата
  4. III. Принципы конечного результата.
  5. III. Требования к результатам освоения содержания дисциплины
  6. III. ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОСВОЕНИЯ СОДЕРЖАНИЯ ДИСЦИПЛИНЫ
  7. IV. Результати інвестиційної, операційної та фінансової діяльності
  8. V. ПОРЯДОК ОФОРМЛЕНИЯ РЕЗУЛЬТАТОВ ИНСПЕКТИРОВАНИЯ МЕСТ ПРИНУДИТЕЛЬНОГО СОДЕРЖАНИЯ
  9. VI. Дайте экспертную оценку результатам испытуемого.
  10. А Порядок работы на станции при тахеометрической съемке. Вычислительная и графическая обработка результатов съемки.
  11. АКТИВНО-ПАССИВНЫЕ ФИНАНСОВО-РЕЗУЛЬТАТНЫЕ СЧЕТА.
  12. Анализ внереализационных финансовых результатов

 

Приклад 1.15. До взуттєвої майстерні для ремонту приносять чоботи і туфлі у співвідношенні 2:3. Ймовірність якісного ремонтування чобіт дорівнює 0,9, а туфель – 0,85. Проведена перевірка якості однієї пари взуття. Виявилося, що ця пара взуття відремонтована якісно. Яка ймовірність того, що це: а) чоботи; б) туфлі.

Розв’язання. Нехай подія А – принесене взуття відремонтовано якісно. Позначимо подію – до ремонту принесли чоботи, – до ремонту принесли туфлі.

Отже, ймовірності гіпотез , .

Умовні ймовірності відповідно дорівнюють

;

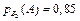
Тоді:

а) ймовірність того, що відремонтованим якісно взуттям є чоботи буде

;

б) ймовірність того, що відремонтованим якісно взуттям є туфлі буде

.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)