АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Властивості математичного сподівання

Читайте также:
  1. А) Властивості бінарних відношень
  2. Атрибутивні ознаки і властивості культури
  3. Б) Основні властивості операцій над множинами
  4. БУДОВА Й ЕЛЕКТРИЧНІ ВЛАСТИВОСТІ НАПІВПРОВІДНИКІВ
  5. Властивості дисперсії
  6. Властивості диференціальної функції
  7. Властивості емпіричної функції
  8. Властивості емпіричної функції розподілу
  9. Властивості інтегральної функції
  10. Властивості ймовірностей подій
  11. Властивості ймовірності
  12. Властивості лінії графіків

1. Математичне сподівання сталої величини дорівнює самій сталій:

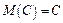
2. Сталий множник можна виносити за знак математичного сподівання:

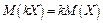
3. Математичне сподівання алгебраїчної суми кінцевого числа випадкових величин дорівнює тій же сумі їх математичних сподівань:

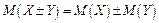
4. Математичне сподівання добутку кінцевого числа незалежних випадкових величин дорівнює добутку їх математичних сподівань

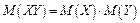
5. Якщо всі значення випадкової величини збільшити (зменшити) на сталу С, то на цю ж сталу збільшиться (зменшиться) математичне сподівання цієї випадкової величини:

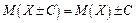
6. Математичне сподівання відхилення випадкової величини від її математичного сподівання дорівнює нулю:

.

 

Дисперсією 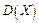випадкової величини Х називається математичне сподівання квадрата її відхилення від математичного сподівання

(1.26)

або

, (1.26′)

де .

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)