Задачі на класичну, статистичну і геометричну ймовірності

1.1. В урні є 10 куль: 3 білих і 7 чорних. З урни навмання виймається одна куля. Яка ймовірність того, що ця куля: а) біла; б) чорна?

1.2. Зі слова «НАВМАННЯ» вибирається навмання одна буква. Яка ймовірність того, що це буква «Я»? Яка ймовірність того, що це гласна?

1.3. Кидають дві гральні кістки. Яка ймовірність випадіння на двох кістках у сумі не менше 9 очок? Яка ймовірність випадіння одиниці, принаймні, на одній кістці?

1.4. Дитина грає з чотирма буквами розрізний абетки А, А, М, М. Яка ймовірність того, що при випадковому розташуванні букв у ряд вона одержить слово «МАМА»?

1.5. При наборі телефонного номера абонент забув дві останні цифри і набрав їх навмання, пам’ятаючи тільки що ці цифри непарні і різні. Знайти ймовірність того, що номер набраний правильно.

1.6. Серед 25 екзаменаційних білетів 5 «гарних». Два студенти по черзі беруть по одному білету. Знайти ймовірності наступних подій: А = {перший студент узяв гарний білет}; В = {другий студент узяв гарний білет}; С = {обидва студенти взяли гарні білети}.

1.7. У партії з 50 виробів 5 бракованих. Навмання вибирається 6 виробів. Визначити ймовірність того, що серед цих 6 виробів 2 бракованих.

1.8. Знайти ймовірність того, що дні народження 12 чоловік прийдуться на різні місяці року.

1.9. У ліфт семиповерхового будинку на першому поверсі ввійшли 3 чоловіки. Кожний з них з однаковою ймовірністю виходить на будь-якому поверху, починаючи з другого. Знайти ймовірності наступних подій: А = {усі пасажири вийдуть на четвертому поверсі); В = {усі пасажири вийдуть одночасно (на одному поверсі)}; С = {усі пасажири вийдуть на різних поверхах).

1.10. У шафі знаходяться 10 пар черевиків різних ґатунків. Випадково вибирають 4 черевики. Знайти ймовірність того, що серед вибраних черевиків відсутні парні.

1.11. У магазин надійшло 30 холодильників, п’ять з них мають заводський дефект. Випадково вибирається один холодильник. Яка ймовірність того, що він не має дефекту?

1.12. В коробці знаходиться шість однакових по формі і близьких по діаметру свердлів. Випадково свердла виймаються з коробки. Яка ймовірність того, що свердла витягнуться в порядку зростання їх діаметра?

1.13. Комісія з якості раз на місяць перевіряє якість продуктів у двох з 30 магазинів, серед яких знаходиться і два відомих вам магазина. Яка ймовірність того, що на протязі місяця вони обидва будуть перевірені?

1.14. На станцію прибули 10 вагонів різної продукції. Вагони позначені номерами від одного до десяти. Знайти ймовірність того, що серед п’яти відібраних для контролю вагонів будуть вагони з номерами 2 і 5?

1.15. З 20 акціонерних товариств (АТ) чотири є банкрутами. Громадянин придбав по одній акції шести АТ. Яка ймовірність того, що серед куплених акцій дві виявляться акціями банкрутів?

1.16. На склад привезли 50 ящиків комплектуючих виробів для одного з видів ЕОМ, але серед них виявилось чотири ящики комплектуючих для іншого виду ЕОМ. Навмання взяли шість ящиків. Знайти ймовірність того, що в одному з цих шести ящиків виявляться некомплектні деталі.

1.17. В партії з 15 однотипних пральних машин 5 машин виготовлені на заводі А, а 10 – на заводі В. Випадково відібрано 5 машин. Знайти ймовірність того, що дві з них виготовлені на заводі А.

1.18. У збирача є 10 деталей, що мало відрізняються одна від одної, з них чотири – першого, по дві – другого, третього і четвертого видів. Яка ймовірність того, що серед шести взятих одночасно деталей три буде першого виду, два – другого і одна – третього?

1.19. 10 студентів умовилися їхати визначеним потягом, але не домовилися про вагон. Яка ймовірність того, що жоден з них не зустрінеться з іншим, якщо в складі потягу 10 вагонів? Передбачається, що всі можливості студентів по вагонах мають рівні ймовірності.

1.20. Серед 17 студентів групи, з яких 8 юнаків розігрується 7 квитків. Яка ймовірність того, що серед власників квитків виявиться 4 дівчини?

1.21. Сім касет розташовуються на полицівипадково. Яка ймовірність того, що 3 касети з записами одного концерту виявляться поруч?

1.22. У шухляді 20 деталей, з них 5 бракованих. Із шухляди навмання виймають 6 деталей. Яка ймовірність того, що з вийнятих деталей дві браковані?

1.23. У шухляді знаходитися50 котушок білого кольору; 20 – чорного, 30 – синього. Чому дорівнює ймовірність того, що 2 узяті навмання котушки будуть: синього кольору; кольорові; не кольорові?

1.24. В урні 15 куль з номерами від 1 до 15. Яка ймовірність витягнути кулю з парним номером? З номером, кратним п’яти?

1.25. Відділ технічного контролю знайшов п’ять бракованих виробів у партії з тисячі виробів. Знайти частоту появи бракованих виробів.

1.26. Після бурі на ділянці між 10-м і 100-м кілометрами телефонної лінії відбувся обрив проводу. Знайти ймовірність того, що обрив відбувся між 35-м і 40-м кілометрами (передбачається рівно можливий розрив в будь-якій точці лінії).

1.27. Куб, усі грані якого пофарбовані, розпиляний на 1000 кубиків однакового розміру. Отримані кубики ретельно перемішані. Визначити ймовірність того, що вийнятий навмання кубик буде мати: а) одну пофарбовану грань; б) дві пофарбовані грані; в) три пофарбовані грані; г) усі не пофарбовані грані.

1.28. У туристів було сім консервних банок (три з м’ясом, дві з овочами і дві з фруктами). Під час дощу етикетки на банках відклеїлися. А усі банки однакові. Яка ймовірність того, що три банки, розкриті навмання, будуть відрізнятися вмістом?

1.29. Оля і Коля домовилися зустріти Новий рік у компанії з десяти чоловік. Вони обоє хотіли сидіти за святковим столом поруч. Знайти ймовірність виконання їхнього бажання, якщо серед друзів прийнято місця розподіляти по жеребкуванню.

1.30. Територія нафтобази має форму прямокутника зі стороною 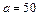м и м. На території мається 4 круглих баки для нафти діаметром 10 м кожний. Яка ймовірність прямої поразки баків бомбою, що потрапила на територію нафтобази, якщо влучення бомби в будь-яку точку однаково ймовірно.

Поиск по сайту: