Перевірка гіпотези про значимість коефіцієнта кореляції

Гіпотеза – лінійного кореляційного зв’язку немає для даної генеральної сукупності.

а) Визначаємо значення критерію, що спостерігається

.

б) по таблиці Ст’юдента визначають .

в) при – нульову гіпотезу відкидають,

при – приймають.

Приклад 2.2. Знайти коефіцієнт кореляції і рівняння лінійної регресії для заданої залежності врожайності (ц/га) від якості ґрунту (у балах). Перевірити коефіцієнт кореляції на значимість.

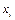
	–1
	–1

Розв’язання. Для зручності обчислень складемо розрахункову таблицю:

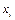
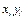
–1	–1
4

Обчислимо середні значення для х і у:

; ; (n= 4)

Обчислимо середні квадратичні відхилення для х і у:

; .

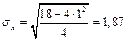Обчислюємо коефіцієнт кореляції:

.

На підставі властивостей коефіцієнта кореляції робимо висновок.

Оскільки r = 0,62 >0, то між x і y сильний, зростаючий лінійний кореляційний зв’язок. Обчислюємо коефіцієнти лінійної регресії :

;

Рівняння лінійної регресії має вигляд:

Побудуємо на координатній площині задані пари точок і отримаємо пряму (рис. 11).

Перевіримо коефіцієнт кореляції на значимість.

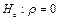– для даної генеральної сукупності лінійного кореляційного зв’язку немає.

а) Обчислюємо значення критерію, що спостерігається

.

б) За таблицею Ст’юдента визначаємо

.

в) Оскільки (1,12 < 4,30) нульову гіпотезу відкидаємо, тобто коефіцієнт кореляції для всієї генеральної сукупності не дорівнює нулю.

Поиск по сайту: