АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Перевірка гетероскедастичності на основі критерію m

Читайте также:
  1. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  2. Визначення величини резерва сумнівних боргів на основі класифікації дебіторської заборгованості
  3. Діяльності «Світового духу» розкривається на основі процесу саморозвитку
  4. Економетрична модель, що будується на основі системи рівнянь, крім регресійних функцій, може включати тотожності.
  5. Змістовний модуль 4. Статистична перевірка гіпотез. Елементи теорії кореляції і дисперсійного аналізу
  6. Інтрапренерство — діяльність з виробництва і реалізації товарів і послуг на основі інтеграції підприємницьких можливостей індивіда і підприємства.
  7. Кредит — це система відносин з приводу акумуляції та використання тимчасово вільних грошових засобів на основі повернення та платності у формі позичкового відсотка.
  8. Математична модель системи управління рухом судна в горизонтальній площини з урахуванням компенсації вітрового збурення на основі закону управління
  9. На основі галузевої структури можна визначити яка це економіка: індустріальна, аграрно-індустріальна, аграрна.
  10. Одержання пароля на основі помилок у реалізації системи
  11. Перевірка
  12. Перевірка відповідності виплат, що включаються у розрахунок середньої заробітної тати.

Цей метод застосовується тоді, коли вихідна сукупність спостережень досить велика. Розглянемо відповідний алгоритм.

Крок 1. Вихідні дані залежної змінної Y розбиваються на k груп відповідно до зміни рівня величини Y.

Крок 2. Закожною групою даних обчислюється сума квадратів відхилень:

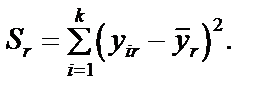
Крок 3. Визначається сума квадратів відхилень в цілому по всій сукупності спостережень:

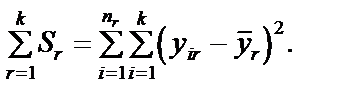
Крок 4. Обчислюється параметр :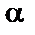

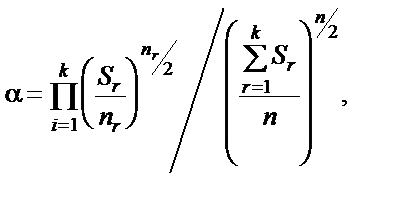
де n — загальна сукупність спостережень; nr — кількість спостережень r -ї групи.

Крок 7. Обчислюється критерій:

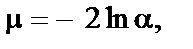
який наближено відповідатиме розподілу при ступені свободи , коли дисперсія всіх спостережень однорідна. Тобто якщо значення не менше за табличне значення при вибраному рівні довіри і ступені свободи , то спостерігається гетероскедастичність.

Приклад Для даних, які наведено в попередньому прикладі, перевіримо наявність гетероскедастичності згідно з критерієм m.

Розв’язання.

Крок 1. Розіб’ємо дані, які наведені в табл., на три групи, по шість спостережень у кожній.

група I група II група III
0,36 0,41 0,82
0,20 0,50 1,04
0,08 0,43 1,53
0,20 0,59 1,94
0,10 0,90 1,75
0,12 0,95 1,99

Крок 2. Обчислимо суму квадратів відхилень індивідуальних значень кожної групи від свого середнього значення:

2.1.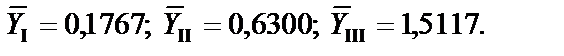

2.2.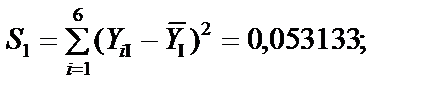

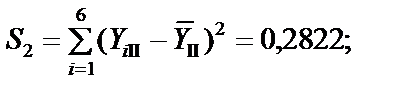
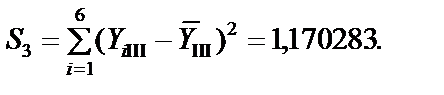
Крок 3. Знайдемо суму квадратів відхилень за всіма трьома групами:

= S 1 + S 2 + S 3 = 0,05313 + 0,2822 + 1,1703 = 1,5056.

Крок 4. Обчислимо параметр

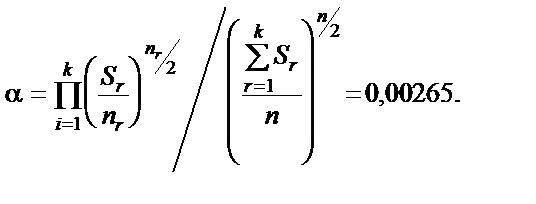
Крок 5. Знайдемо критерій

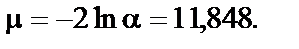
Цей критерій наближено задовольняє розподіл c2 з k – 1 = 2 ступенями свободи. Порівняємо значення критерію з табличним значенням критерію c2 з k – 1 = 2 ступенями свободи при рівні довіри 0,99 c2кр= 9,21. Оскільки m > c2кр, то дисперсія може змінюватись, тобто для даних табл. 7.1 спостері­гається гетероскедастичність.


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.005 сек.)