Оцінка тісноти та значимості зв’язку між змінними у рівняннях парної регресії

Після вибору виду рівняння регресії та знаходження його параметрів розпочинають другий етап – кореляційний аналіз, тобто дають оцінку тісноти та значимості зв’язку змінних у регресійній моделі. У поняття «тіснота зв’язку» (щільність) вкладається оцінка

Впливу незалежної змінної на залежну. Під терміном «значимість зв’язку» розуміють оцінку відхилення вибіркових змінних від своїх значень у генеральній сукупності спостережень за допомогою статистичних критеріїв.

Для характеристики тісноти та значимості зв’язку зручно користуватися перетвореними виразами дисперсій для розглядаємих коефіцієнтів.

Тісноту зв’язку між залежною змінною у та незалежною змінною х оцінюють за допомогою таких характеристик: коефіцієнт детермінації; коефіцієнт кореляції (індекс кореляції). За допомогою цих коефіцієнтів перевіряється відповідність побудованої регресійної моделі (теоретичної) фактичним даним.

Коефіцієнт детермінації показує, якою мірою варіація залежної змінної у визначається варіацією незалежної змінної х. Він використовується як при лінійному, так і нелінійному зв’язку між змінними та розраховується за формулою

,

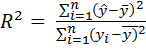Де 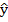– теоретичне значення залежної змінної на підставі побудованої регресійної моделі; – загальна середня фактичних даних результативного показника; у_і – фактичні індивідуальні значення результативного показника.

Коефіцієнт детермінації приймає значення від 0 (відсутній лінійний зв’язок між показниками) до 1 (відсутній кореляційний зв’язок між показниками).

Коефіцієнт кореляції, або індекс кореляції, показує, наскільки значним є вплив змінної х_і на у_і і розраховується так:

Чим ближче коефіцієнт кореляції до 1, тим тісніше зв’язок між незалежною та залежною змінними.

Іноді для спрощення розрахутків тісноту кореляційного зв’язку характеризують коефіцієнтом кореляції, який розраховують за формулою:

Якщо зв’язок між результативними і вхідними показниками лінійний, то використовується лінійний коефіцієнт кореляції, який характеризує не тільки тісноту зв’язку, а й його напрям:

Де n – число фактичнизначень у_і; х_і – фактичні індивідуальні значення вхідного показника.

Коефіцієнт кореляції набуває значень від -1 до +1. При достатніх значеннях коефіцієнта кореляції із зростанням факторної змінної збільшується середнє значення результуючої змінної; при від’ємних – із зростанням факторної змінної середнє значення результуючої змінної зменшується. Знак коефіцієнта кореляції збігається зі знаком коефіцієнта регресії. При r = 0 змінні не можуть мати лінійного кореляційного зв’язку. Ступінь тісноти їх лінійної залежності зростає при наближені r до+-1. Кореляційний зв'язок між показниками відсутній при r=+-1. Коли r 0, то зв’язок між показниками прямий, якщо r 0, то зв’язок обернений. Можуть бути визначені стандартні похибки оцінок параметрів моделі з урахуванням дмсперсії залишків:

, де – дисперсія залишків

;

– елемент матриці похибок С (матриця, обернена до матриці коефіцієнтів системи нормальних рівнянь); m₁ – кількість параметрів моделі.

В залежності від значення стандартної похибки робиться висновок про ступінь незміщеності оцінок параметрів.

Після встановлення тісноти зв’язку між змінними моделі характеризують значимість зв’язку, яка в кореляційному аналізі частіше всього здійснюється за допомогою F-критерія Фішера. У випадку парної регресії цей критерій розраховується за формулою:

Де 1,(n-2) – число ступенів вільності відповідно чисельника і знаменника залежності.

Під терміном «ступенів вільності» в економетрії розуміють число, яке показує, скільки незалежних елементів інформації із змінних у_і (і-1...n) потрібно для розрахунку розглядаємої суми квадратів. В кореляційному аналізі існує рівняння, яке пов'язує відхилення загальної суми квадратів із залишковою сумою квадратів та сумою квадратів, що пояснює регресію:

S_y=S_e+S_Y?

Де S_y – загальна сума квадратів відхилень,

;

S_e – залишкова сума квадратів відхилень,

;

S_Y – регресійна сума квадратів відхилень,

Кожна із зазначених сум пов’язана з ступенями вільності: для загальної суми квадратів S_y потрібно (n-1) незалежних чисел, тобто ступенів вільності; для залишкової суми квадратів S_e –(n-m₁) степенів вільності; для регресійної суми квадратїв S_Y – (m₁-1) степенів вільності.

За статистичними таблицями F-розподілу Фішера із степенями вільності 1, (n-2) і рівнем довіри (1-α) вибирається F_табл. Можлива помилка (рівень значущості) α може прийматися 0,05 або 0,01. Це означає, що у 5% або 1% випадків ми можемо помилитися, а у 95% або 99% випадків (рівень довіри) наші висновки будуть правильними. При умові F F_табл. побудована регресійна модель відповідає реальній дійсності.

Приклад. За даними попередньої задачі оцінити тісноту та значимість зв’язку між змінними.

Розв’язання. Допоміжні розрахунки до визначення характеристик тісноти та значимості зв’язку зручно проводити у табличній формі:

№	x	y				u=y-	u2=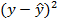
			16.67	28.41		0.33	0.1089
			18.31	13.62		-0.31	0.0961
			19.31	7.24		-0.31	0.0961
			19.95	4.20		0.05	0.0961
			21.59	0.17		-0.59*	0.3481
			22.41	0.17		0.59	0.3481
			24.05	4.20		-0.05	0.0025
			24.87	8.24		0.13	0.0169
			25.69	13.62		0.31	0.0961
			27.33	28.41		-0.33	0.1089
∑			-	108.28		-	1.224

Дамо оцінку тісноти зв’язку між змінними моделі.

Коефіцієнт детермінації розрахуємо за формулою:

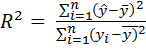= =0,984.

Значення коефіцієнта детермінації свідчить про те, що зв’язок між змінними у прикладі тісний (відмінність від 1 складає 1,6%). Значення 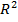показує, що варіація роздрібного товарообігу на 98,4% визначається варіацією доходів населення, а 1,6% - вплив неврахованих факторів.

Коефіцієнт кореляції розраховується за формулою

= = 0,992.

Значення коефіцієнта кореляції R=0,992 свідчить, що існує тісний зв’язок між цими соціально-економічними показниками (R наближається до 1).

Коефіцієнт кореляції за формулою

= = 0,994

Показує, що знайдене значення практично співпадає з розрахованим за попередньою формулою.

Значення R² та R для парної регресії економетричної моделі свідчить про достатню тісноту зв’язку, так як вони наближені до одиниці.

Знайдемо матрицю похибок С, яка є оберненою до матриці коефіцієнтів системи нормальних рівнянь А:

А= ; С=А^-1 =

Визначимо стандартні похибки оцінок параметрів моделі з урахуванням дисперсії залишків:

=

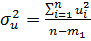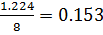
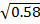= = =0.761;

= =0.030/

Порівняємо стандартні похибки оцінок параметрів з їх значеннями =1,91 і 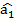=0,82. Так стандартна похибка оцінки параметра становить 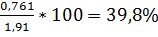абсолютного значення цієї оцінки (1,91), а тому цей параметр може мати зміщення, яке зумовлене невеликою сукупністю спостережень (n=10). Стандартна похибка оцінки параметра 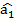становить абсолютного значення оцінки (0,82), що свідчить про незміщеність такої оцінки параметра моделі.

Тепер оцінемо значимість зв’язку між змінними моделі за допомогою F-критерія Фішера.

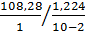= = 707,8.

Обчислене фактичне значення критерія Фішера F порівнюється з табличним F_табл. При ступенях вільності чисельника (1) та знаменника (n-2)=(10-2)=8 при прийнятому рівню значимості α=0,05 та рівню довіри (1-α)=(1-0,05)=0,95 F_табл =5,32. Так як F F_табл (707,8 5,32), то це означає значимість зв’язку між змінними в економетричній моделі.

Поиск по сайту: