АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Коефіцієнт регресії та його властивості

Читайте также:
  1. Баланс часу зміни та коефіцієнт використання часу зміни
  2. Встановлення коефіцієнтів запасу міцності
  3. Головними коефіцієнтами
  4. Зварювальна дуга і її властивості.
  5. Знаходження параметів лінійного рівняння регресії методом найменших квадратів
  6. І. Метод коефіцієнта використання світлового потоку або метод коефіцієнта використання освітлювальної установки.
  7. Коефіцієнт небезпеки
  8. Коефіцієнти переведення фізичного поголів'я тварин в умовні голови великої рогатої худоби
  9. Криві байдужості та їх властивості.
  10. Культурно-історичний процес, його основні принципи та властивості.
  11. Лінійна кореляція і рівняння лінійної регресії

В теорії ймовірностей та математичній статистиці, кореляція є залежністю двох випадкових величин. При цьому, зміна однієї або кількох цих величин призводить до систематичної зміни іншої або інших величин. Математичною мірою кореляції двох випадкових величин слугує коефіцієнт кореляції.

Кореляція може бути позитивною та негативною (можлива також ситуація відсутності статистичного зв'язку - наприклад, для незалежних випадкових величин). Від'ємна кореляція – кореляція, при якій збільшення однієї змінної пов'язане зі зменшенням іншої, при цьому коефіцієнт кореляції від'ємний. Додатна кореляція – кореляція, при якій збільшення однієї змінної пов'язане зі збільшенням іншої, при цьому коефіцієнт кореляції додатній.

Нехай та 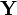— випадкові величини з математичним сподіванням μ X та μ Y. Їх коефіцієнт кореляції позначається як і дорівнює:[1]

де:

— коваріація величин та ,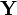

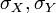— стандартне відхилення величин та ,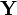

— оператор математичного сподівання.

Якщо X та Y — незалежні, то коефіцієнт кореляції дорівнює 0. Зворотне твердження невірне. Коефіцієнт кореляції може дорівнювати 0 навіть якщо Y є функцією від X.

Завжди виконується нерівність:

.

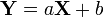Причому, тоді і лише тоді, коли , де a та b — сталі.

 

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.002 сек.)