 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Нормальний закон розподілу
Означення. Нормальним називається розподіл ймовірностей неперервної випадкової величини, якщо її густина розподілу має вигляд:
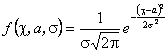 (12)
(12)
для довільного значення  і довільних чисел
і довільних чисел  і
і  .
.
Числа  і
і  називають параметрами розподілу і мають певний ймовірнісний зміст, який розглянемо нижче.
називають параметрами розподілу і мають певний ймовірнісний зміст, який розглянемо нижче.
Графіком функції (12) є крива, яку в літературі називають кривою Гаусса, або нормальною кривою.
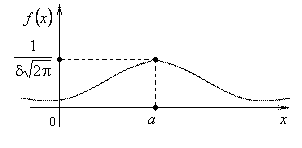

Якщо у формулі (12) покласти 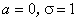 , отримуємо нормовану функцію Гаусса, яка нам уже траплялася в теоремах Муавра-Лапласа (див. лк.23, §3) під назвою функції Лапласа.
, отримуємо нормовану функцію Гаусса, яка нам уже траплялася в теоремах Муавра-Лапласа (див. лк.23, §3) під назвою функції Лапласа.
Бачимо, що нормальний розподіл визначається двома параметрами:  і
і  . Досить знати ці параметри, щоб задати нормальний закон розподілу. Доведемо, що ймовірнісний зміст цих параметрів наступний:
. Досить знати ці параметри, щоб задати нормальний закон розподілу. Доведемо, що ймовірнісний зміст цих параметрів наступний:  - математичне сподівання, а
- математичне сподівання, а  - середнє квадратичне відхилення.
- середнє квадратичне відхилення.
32. Нормальний закон розподілу: формули обчислення ймовірностей та правило 3-х сигма.
….Запишемо різні форми відомої формули Пуассона:
I. 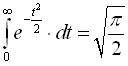 ;
;
II. 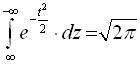 ; (3.1)
; (3.1)
III. 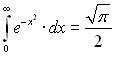 .
.
Інтеграл ймовірностей має властивості:
1) 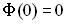 ;
;
2) 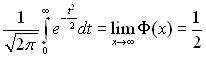 ;
;  .
.
3) 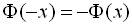 , інтеграл ймовірностей ‑ непарна функція.
, інтеграл ймовірностей ‑ непарна функція.

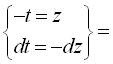
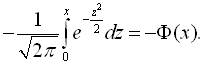
Нехай 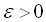 . Знайдемо імовірність того, що нормально розподілена випадкова величина
. Знайдемо імовірність того, що нормально розподілена випадкова величина 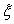 відхиляється від параметра а за абсолютною величиною не більше, ніж на
відхиляється від параметра а за абсолютною величиною не більше, ніж на 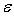 , тобто
, тобто 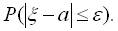 Нерівність
Нерівність 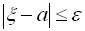 рівносильна нерівностям
рівносильна нерівностям  . Беремо в рівності (3. 2)
. Беремо в рівності (3. 2) 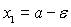 ,
, 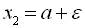 і одержимо:
і одержимо:

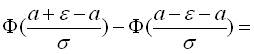
 ,
,
Внаслідок того, що інтеграл ймовірностей непарна функція:
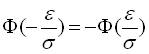 .
.
Тому 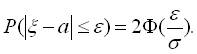 (3.3)
(3.3)
Одержаний факт означає: якщо в. в. підпорядковується нормальному закону розподілу, то можна стверджувати, що з імовірністю 0,9973 в. в. знаходиться в інтервалі 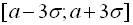 .
.
Дана ймовірність наближається до одиниці, тому вважають, що значення нормально розподіленої в. в. практично не виходять за границі інтервалу 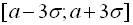 . Цей факт називають “правилом трьох сигм”.
. Цей факт називають “правилом трьох сигм”.
Для нормально розподіленої в. в. всі відхилення (з точністю 0,9973) знаходяться на інтервалі 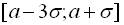 .
.
З правила трьох сигм випливає спосіб визначення середнього квадратичного відхилення: беруть максимальне практично можливе відхилення від середнього і ділять на три. Таке грубе обчислення рекомендують у випадку, коли немає інших способів визначення 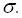
33. Статистичні розподіли вибірок та їх числові характеристики: загальна інформація.
Кожна непорожня підмножина А множини (Ω) випадково вибраних елементівіз генеральної сукупності називається вибіркою.
Кількість усіх елементів вибірки називають її обсягом і позначається n.
Коли реалізується вибірка, кількісна ознака, наприклад Х, набуває конкретних числових значень (Х = хі), які називають варіантою.
Зростаючий числовий ряд варіант називають варіаційним.
Кожна варіанта вибірки може бути спостереженою ni раз (ni 1), число³ ni називають частотою варіантиxi.
При цьому
 , (350)
, (350)
де k — кількість варіант, що різняться числовим значенням;
n — обсяг вибірки.
Відношення частоти ni варіанти xi до обсягу вибірки n називають її відносною частотою і позначають через Wi, тобто
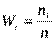 .
.
Для кожної вибірки виконується рівність
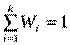 .
.
Якщо досліджується ознака генеральної сукупності Х, яка є неперервною, то варіант буде багато. У цьому разі варіаційний ряд — це певна кількість рівних або нерівних частинних інтервалів чи груп варіант зі своїми частотами.
Такі частинні інтервали варіант, які розміщені у зростаючій послідовності, утворюють інтервальний варіаційний ряд.
На практиці для зручності, як правило, розглядають інтервальні варіаційні ряди, у котрих інтервали є рівними між собою.
34. Дискретний статистичний розподіл вибірки
та її числові характеристики
Перелік варіант варіаційного ряду і відповідних їм частот, або відносних частот, називають дискретним статистичним розподілом вибірки.
У табличній формі він має такий вигляд:
| X = xi | x 1 | x 2 | x 3 | … | xk |
| ni | n 1 | n 2 | n 3 | … | nk |
| Wi | W 1 | W 2 | W 3 | … | Wk |
Дискретний статистичний розподіл вибірки можна подати емпіричною функцією F *(x).
Емпірична функція F *(x) та її властивості. Функція аргументу х, що визначає відносну частоту події X < x, тобто
 , (353)
, (353)
називається емпіричною, або комулятою.
n — обсяг вибірки;
nx — кількість варіант статистичного розподілу вибірки, значення яких менше за фіксовану варіанту х;
F *(x) — називають ще функцією нагромадження відносних частот.
Властивості F *(x):
1) 0 £ F *(x)£1
2) F (x min) = 0, де x min є найменшою варіантою варіаційного ряду;
3) 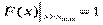 , де x max є найбільшою варіантою варіаційного ряду;
, де x max є найбільшою варіантою варіаційного ряду;
4) F (x) є неспадною функцією аргументу х, а саме: F (x 2)³ F (x 1) при x 2 ³ x 1
Полігон частот і відносних частот. Дискретний статистичний розподіл вибірки можна зобразити графічно у вигляді ламаної лінії, відрізки якої сполучають координати точок (xi; ni), або (xi; Wi).
У першому випадку ламану лінію називають полігоном частот, у другому — полігоном відносних частот.
Числові характеристики:
1) Вибіркова середня величина. Величину, яка визначається формулою називають вибірковою середньою величиною статистичного розподілу вибірки.
 xi — варіанта варіаційного ряду вибірки;
xi — варіанта варіаційного ряду вибірки;
ni — частота цієї варіанти;
n — обсяг вибірки (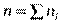 ).
).
Якщо всі варіанти з’являються у вибірці лише по одному разу, тобто ni =1, то
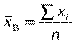
2) відхилення варіант. Різницю (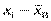 ) ni називають відхиленням варіант.
) ni називають відхиленням варіант.
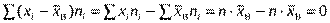 .
.
Отже, сума відхилень усіх варіант варіаційного ряду вибірки завжди дорівнює нулеві;
3) мода (Mo*). Модою дискретного статистичного розподілу вибірки називають варіанту, що має найбільшу частоту появи.
Мод може бути кілька. Коли дискретний статистичний розподіл має одну моду, то він називається одномодальним, коли має дві моди — двомодальним і т. д.;
4) медіана (Me*). Медіаною дискретного статистичного розподілу вибірки називають варіанту, яка поділяє варіаційний ряд на дві частини, рівні за кількістю варіант;
5) дисперсія. Для вимірювання розсіювання варіант вибірки відносно 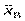 вибирається дисперсія.
вибирається дисперсія.
Дисперсія вибірки — це середнє арифметичне квадратів відхилень варіант відносно 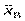 , яке обчислюється за формулою
, яке обчислюється за формулою
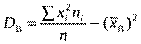
6) середнє квадратичне відхилення вибірки sB. При обчисленні D B відхилення підноситься до квадрата, а отже, змінюється одиниця виміру ознаки Х, тому на основі дисперсії вводиться середнє квадратичне відхилення
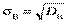
яке вимірює розсіювання варіант вибірки відносно 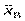 , але в тих самих одиницях, в яких вимірюється ознака ^ Х;
, але в тих самих одиницях, в яких вимірюється ознака ^ Х;
7) розмах (R). Для грубого оцінювання розсіювання варіант відносно 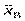 застосовується величина, яка дорівнює різниці між найбільшою x max і найменшою x min варіантами варіаційного ряду. Ця величина називається розмахом
застосовується величина, яка дорівнює різниці між найбільшою x max і найменшою x min варіантами варіаційного ряду. Ця величина називається розмахом
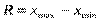 ; (359)
; (359)
8) коефіцієнт варіації V. Для порівняння оцінок варіацій статистичних рядів із різними значеннями 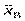 , які не дорівнюють нулеві, вводиться коефіцієнт варіації, який обчислюється за формулою
, які не дорівнюють нулеві, вводиться коефіцієнт варіації, який обчислюється за формулою
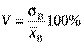
35. Інтервальний статистичний розподіл
вибірки та його числові характеристики
Перелік часткових інтервалів і відповідних їм частот, або відносних частот, називають інтервальним статистичним розподілом вибірки.
У табличній формі цей розподіл має такий вигляд:
| h | x 1 – x 2 | x 2 – x 3 | x 3 – x 4 | … | xk –1 – xk |
| ni | n 1 | n 2 | n 3 | … | Nk |
| Wi | W 1 | W 2 | W 3 | … | Wk |
Тут h = xi – xi –1 є довжиною часткового i -го інтервалу. Як правило, цей інтервал береться однаковим.
Інтервальний статистичний розподіл вибірки можна подати графічно у вигляді гістограми частот або відносних частот, а також, як і для дискретного статистичного розподілу, емпіричною функцією F *(x) (комулятою).
Гістограма частот та відносних частот. Гістограма частот являє собою фігуру, яка складається з прямокутників, кожний з яких має основу h і
висотy 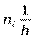 .
.
Гістограма відносних частот є фігурою, що складається з прямокутників, кожний з яких має основу завдовжки h і висоту, що дорівнює 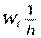 .
.
Емпірична функція F *(x) (комулята). При побудові комуляти F *(x) для інтервального статистичного розподілу вибірки за основу береться припущення, що ознака на кожному частинному інтервалі має рівномірну щільність імовірностей. Тому комулята матиме вигляд ламаної лінії, яка зростає на кожному частковому інтервалі і наближається до одиниці.
Аналогом емпіричної функції F *(x) у теорії ймовірностей є інтегральна функція F (x) = P (X < x).
Медіана. Для визначення медіани інтервального статистичного розподілу вибірки необхідно визначити медіанний частковий інтервал. Якщо, наприклад, на і -му інтервалі [ xi –1 – xi ] F *(xi –1) <0,5i F *(xi)> 0,5, то, беручи до уваги, що досліджувана ознака Х є неперервною і при цьому F *(x) є неспадною функцією, всередині інтервалу [ xi –1 – xi ] неодмінно існує таке значення X =Me, де F * (Me) = 0,5.
Мода. Для визначення моди інтервального статистичного розподілу необхідно знайти модальний інтервал, тобто такий частинний інтервал, що має найбільшу частоту появи.
Використовуючи лінійну інтерполяцію, моду обчислимо за формулою
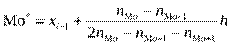 , (362)
, (362)
де xi –1 — початок модального інтервалу;
h — довжина, або крок, часткового інтервалу;
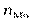 — частота модального інтервалу;
— частота модального інтервалу;
 — частота домодального інтервалу;
— частота домодального інтервалу;
 — частота післямодального інтервалу.
— частота післямодального інтервалу.
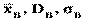 для інтервального статистичного розподілу вибірки. Для визначення
для інтервального статистичного розподілу вибірки. Для визначення  перейдемо від інтервального розподілу до дискретного, варіантами якого є середина часткових інтервалів
перейдемо від інтервального розподілу до дискретного, варіантами якого є середина часткових інтервалів 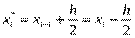 і який має такий вигляд:
і який має такий вигляд:

| 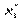
| 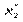
| 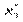
| … | 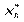
|
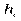
| 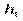
| 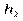
| 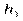
| … | 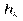
|
Тоді 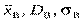 обчислюються за формулами:
обчислюються за формулами:
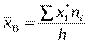

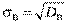 .
.
Поиск по сайту: