АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Двовимірний статистичний розподіл вибірки та його числові характеристики

Читайте также:
  1. I. Схема характеристики.
  2. IX. У припущенні про розподіл ознаки по закону Пуассона обчислити теоретичні частоти, перевірити погодженість теоретичних і фактичних частот на основі критерію Ястремського.
  3. V. Для дискретної випадкової величини Х, заданої рядом розподілу, знайти:
  4. Біноміальний закон розподілу
  5. Виды технических обслуживаний (ТО), их периодичность, простои в них, характеристики.
  6. Визначення мінімально достатнього обсягу вибірки
  7. Визначення необхідної чисельності вибірки.
  8. Випадкові величини та їх розподіл
  9. Випадкові змінні х та у стохастично залежні, якщо зміна однієї з них викликає зміну розподілу другої (умовний розподіл однієї з них залежить від значень другої).
  10. Випадкові події і величини, їх числові характеристики
  11. Властивості емпіричної функції розподілу
  12. Властивості функції розподілу

Перелік варіант та відповідних їм частот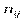
спільної їх появи утворюють двовимірний статистичний розподіл вибірки, що реалізована з генеральної сукупності, елементам цієї вибірки притаманні кількісні ознаки Х і Y.
У табличній формі цей розподіл має такий вигляд:

…
…
…
…
… … … … … … …
…
…  

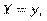
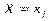
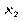
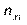
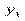
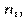
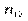
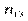
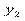
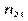
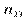
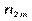
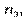
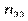
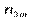
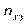
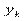
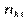
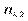
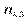
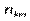
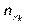
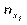
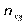
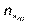
Тут — частота спільної появи варіант


.

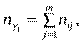
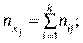
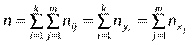Загальні числові характеристики ознаки Х:
1)загальна середня величина ознаки Х

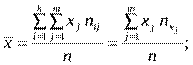
2)загальна дисперсія ознаки Х


3)загальне середнє квадратичне відхилення ознаки Х

Загальні числові характеристики ознаки Y:
1)загальна середня величина ознаки Y

2)загальна дисперсія ознаки Y

3)загальне середнє квадратичне відхилення ознаки Y

Умовні статистичні розподіли та їх числові характеристики
Умовним статистичним розподілом ознаки Y при фіксованому значенні 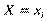називають перелік варіант ознаки ^ Y та відповідних їм частот, узятих при фіксованому значенні Х.

.

…
…


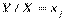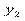
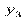
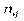
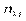
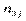
Тут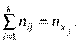
Числові характеристики для такого статистичного розподілу називають умовними. До них належать:
1)умовна середня ознаки Y

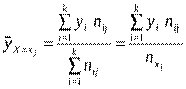
2)умовна дисперсія ознаки Y

3)умовне середнє квадратичне відхилення ознаки Y

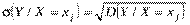
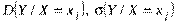вимірюють розсіювання варіант ознаки Y щодо умовної середньої величини

Умовним статистичним розподілом ознаки Х при 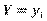називають перелік варіант 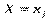та відповідних їм частот, узятих при фіксованому значенні ознаки .

.

…
…


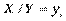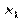
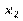
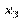
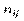
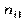
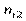
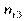
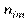
Тут
Умовні числові характеристики для цього розподілу:
1)умовна середня величина ознаки Х

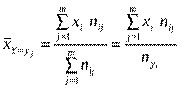
2)умовна дисперсія ознаки Х

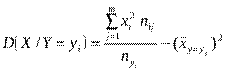
3)умовне середнє квадратичне відхилення ознаки Х
.

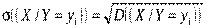При відомих значеннях умовних середніх загальні середні ознаки Х та Y можна обчислити за формулами:


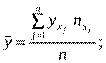
Кореляційний момент, вибірковий коефіцієнт кореляції
Під час дослідження двовимірного статистичного розподілу вибірки постає потреба з’ясувати наявність зв’язку між ознаками Х і Y, який у статистиці називають кореляційним. Для цього обчислюється емпіричний кореляційний момент 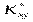за формулою
.
Якщо 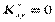, то кореляційного зв’язку між ознаками Х і Y немає. Якщо ж 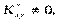то цей зв’язок існує.
Отже, кореляційний момент дає лише відповідь на запитання: є зв’язок між ознаками Х і Y, чи його немає.
Для вимірювання тісноти кореляційного зв’язку обчислюється вибірковий коефіцієнт кореляції 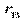за формулою
.
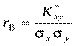Як і в теорії ймовірностей,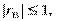


 

 


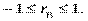
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)