Перевірка статистичних гіпотез

Статистичною називають гіпотезу про вигляд невідомого розподілу або про параметри невідомих розподілів.

Перевірку гіпотез на основі вибіркових статистичних даних називають статистичною перевіркою гіпотез.

Одну з висунутих гіпотез виділяють в ролі основної і позначають, як правило Н₀ (нульова), поряд з нею висувають альтернативну (конкуруючу) гіпотезу, яка суперечить основній і позначають Н₁.

Розрізняють також гіпотези за кількістю припущень. Простою називається гіпотеза, що має лише одне припущення, інакше гіпотеза є складною, тобто складається зі скінченного чи нескінченного числа простих гіпотез.

Може бути прийняте неправильне рішення, тобто можуть бути допущені помилки двох родів.

Помилка першого роду полягає в тому, що буде відхилена правильна гіпотеза.

Помилка другого роду полягає в тому, що буде прийнята неправильна гіпотеза.

Правильне рішення може бути прийняте також у двох випадках:

а) гіпотеза приймається, причому і в дійсності вона правильна;

б) гіпотеза відхиляється, причому і в дійсності вона неправильна.

Ймовірність здійснити помилку першого роду позначають через a і називають її рівнем значимості. Число aзадають малим і найчастіше використовують значення a, що дорівнюють 0,05; 0,001 і т.д. Якщо, наприклад, a=0,01, то це означає, що в одному випадку зі 100 є ризик допустити помилку першого роду (відхилити гіпотезу Н₀).

Оскільки зараз конкретний вигляд розподілу до уваги не береться, то позначають цю величину взагалі через К.

Статистичним критерієм (просто критерієм) називають випадкову величину К, що служить для перевірки нульової гіпотези. Для різних гіпотез ці критерії є різними.

Найбільш розповсюдженим критерієм перевірки гіпотези Н₀ про закон розподілу ознаки генеральної сукупності є критерій узгодженості:

де m – число інтервалів, на які розбита вибірка, n – об’єм вибірки, n_i – частота і-го інтервалу, r_і – ймовірність попадання значень ознаки в і-ий інтервал, яка обчислюється для теоретичного закону розподілу.

Спостережуваним значенням К_сп називається значення критерію, обчислене по результатах вибірки.

Всю множину значень статистичного критерію К можна розбити на дві підмножини, що не перетинаються А і Ā.

Значення статистичного критерію підмножини А Î , при яких нульова гіпотеза приймається, називається областю прийняття гіпотези, а підмножина значень Ā, при яких гіпотеза Н₀ відхиляється – критичною областю.

Основний принцип перевірки статистичних гіпотез формується так: якщо спостережуване значення критерію К_сп­належить області прийняття гіпотези А – гіпотезу приймають, якщо К_сп­ належить критичній області Ā гіпотезу відхиляють.

Оскільки критерій К – одномірна випадкова величина, то всі її можливі значення належать деякому інтервалу. Тому область прийняття гіпотези А і критична область Ā також є інтервальними, а, значить, існують точки, котрі їх розділяють і називають критичними і позначаються k_кр.

Розрізняють:

Правосторонньою називають критичну область, що визначається нерівністю К > k_кр, де k_кр – додатне число

Лівосторонньою називають критичну область, що визначається нерівністю К < k_кр, де k_кр < 0

Двосторонньою називають критичну область, що визначається нерівністю К < k_1кр, К > k_2кр, де k₂ >

Перевірка статистичних гіпотез будь-якої природи здійснюється за такою схемою:

1. Формулюється статистична гіпотеза Н₀.

2. Вибирається статистичний критерій відповідно до сформульованої нульової гіпотези Н₀.

3. Залежно від гіпотези Н₀ і альтернативної Н₁ вибирається одностороння або двостороння критична область.

Щоб побудувати критичні області, необхідно знайти значення критичних точок.

4. За результатами вибірки обчислюється спостережене значення критерію К_сп.

5. Виходячи з вимоги, що при правильності гіпотези Н₀ ймовірність того, що К_сп потрапить у критичну область, має дорівнювати прийнятому рівню значимості a, перевіряється статистична гіпотези.

Це твердження подають для лівосторонньої критичної області так:

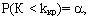
для правосторонньої:

для двосторонньої критичної області:

Поиск по сайту: