Перевірка гіпотези про закон розподілу. Критерій згоди Пірсона

Критерієм згоди називають статистичний критерій перевірки гіпотези про закон розподілу ймовірностей випадкової величини (ознаки генеральної сукупності). Є кілька критеріїв згоди: критерій Колмогорова, критерій Смірнова, критерій Пірсона та ін.

Найбільш розповсюдженим критерієм перевірки вірогідності H про закон розподілу ознаки генеральної сукупності є критерій згоди Пірсона (критерій ), який ґрунтується на порівнянні емпіричних і теоретичних частот та визначається за формулою , де m – число інтервалів, на які поділяється статистичний розподіл вибірки; n_і – частота ознаки в i –му інтервалі; п_і* – теоретичні частоти, підраховані за відповідними формулами закону розподілу ймовірностей, який припускається для ознаки генеральної сукупності.

Теоретичні частоти знаходяться за формулою , де n – об’єм вибірки; p_i – для дискретної випадкової величини є ймовірність події Х= х; для неперервної випадкової величини – ймовірність, що ознака Х попаде в і-ий інтервал.

Нехай висунуто гіпотезу H ₀: випадкова величина Х розподілена за законом А.

Здійснивши вибірку обсягу п, знаходять і записують у вигляді таблиці інтервальний статистичний розподіл частот:

				...
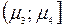
ni	n1	n2	n3	...	nm

Оскільки перевіряється гіпотеза про те, що розподіл ознаки Х генеральної сукупності описується певною (конкретною) функцією розподілу F (x), то для кожного інтервалу можна визначити теоретичні ймовірності p_i попадання значень випадкової величини Х у цей інтервал, а отже, і теоретичні частоти .

Для обчислення ймовірностей p_i використовують формули:

(26)

Зазначимо, що для обчислення ймовірностей p_i і p_m у формулі (26) покладають, відповідно, і . Тоді .

Отримані результати обчислень зручно записати у формі таблиці:

				...
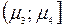
ni	n1	n2	n3	...	nm
pi	p1	p2	P3	...	pm
	n1*	n2*	n3*	...	nm*

Згідно з критерієм Пірсона для перевірки гіпотези H₀ вводиться випадкова величина (статистика) K:

На підставі даних вибірки, записаних у таблиці, обчислюють емпіричне значення критерію Пірсона:

Відомо, що при n → ∞ закон розподілу статистики K прямує до закону розподілу з k = m − r −1 ступенями вільності, де m – кількість груп у статистичному розподілі вибірки; r − кількість параметрів гіпотетичного розподілу A (наприклад, r = 2 для нормального розподілу, r =1 для розподілу Пуассона, r =0 для рівномірного розподілу).

Для критерію будують правосторонню критичну область за правилом:

P{ > _кр.}=a (27)

За заданим рівнем значущості α і кількістю ступенів вільності k із таблиці критичних точок розподілу (в якій дано розв’язки рівняння (27)) знаходять критичну точку k _кр=(a, k).

Порівнюємо значення k_кр і К_спост: якщо К_спост ≥ k_кр то гіпотезу H₀ відхиляють; якщо ж К_спост < k_кр, то гіпотезу H₀ приймають.

Застосування критерію вимагає дотримання таких умов:

1) експериментальні дані мають бути незалежними, тобто вибірка має бути випадковою;

2) обсяг вибірки має бути достатньо великим (практично не меншим ніж 50 одиниць), а частота кожної групи – не меншою за 5. Якщо остання умова не виконується, то проводиться попереднє об’єднання нечисленних груп.

Критерій згоди Пірсона дає відповідь на питання, чи розбіжність між емпіричними і теоретичними частотами зумовлена випадковістю, чи вона є значущою. Як і будь-який інший критерій він не доводить справедливостігіпотези H₀, а лише дозволяє встановити на прийнятному рівні значущості узгодженість чи неузгодженість гіпотези H₀, з даними спостережень.

Приклад. При рівні значущості перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти

Розв’язання

Складаємо таблицю для обчислення -критерію.

і		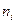пі*
					2,25		12,25
			-1		0,07		13,06
			-4		0,37		35,37
			-8		0,77		67,77
					0,49		114,49
					1,05		96,05
			-7		1,29		25,28
					0,07		16,07
							380,34

Контроль обчислень: – обчислення правильні.

Кількість ступенів вільності: s=8, k=s-3=5. За таблицею критичних точок -розподілу (додаток 4) за рівнем значущості і кількістю ступенів вільності k=5 знаходимо . Оскільки , то немає підстав відхилити нульову гіпотезу. Отже, розбіжність емпіричних та теоретичних частот незначуща, дані спостережень узгоджуються з гіпотезою про нормальний розподіл генеральної сукупності.

Поиск по сайту: