АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Практичне заняття №14

Читайте также:
  1. V. Зміст теми заняття.
  2. VI. Матеріали методичного забезпечення заняття
  3. За практичні заняття
  4. Заняття 1. Оцінка впливу небезпечних речовин, що забруднили
  5. Заняття 1.Вступ. Цілі та задачі предмету. Короткі відомості з розвитку електрики.
  6. Заняття 14. Основні властивості та характеристики МП. Правило правохідного гвинта.
  7. Заняття 15. ЕМ сила. Правило лівої руки. Поняття про ДПС.
  8. Заняття 17. Індуктивність.Явище самоіндукції.
  9. Заняття 23. Спосіб отримання трьохфазної системи напруг та струмів. Трьохфазний генератор.
  10. Заняття 24 . З”єднання джерела та приймача енергії зіркою.
  11. Заняття 3. Потік вектора напруженості електричного поля. Теорема Гауса
  12. Заняття 4. Електрична напруга,потенціал,різниця потенціалів

Тема: Точкові та інтервальні оцінки

Мета: сформувати у студентів уявлення про точкові та інтервальні оцінки, навчити знаходити довірчі інтервали для математичного сподівання, дисперсії та середнього квадратичного відхилення.

План заняття

1. Точкові оцінки. Інтервальні оцінки.

2. Довірчі інтервали для математичного сподівання.

3. Довірчі інтервали для дисперсії.

рекомендована Література

1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 219-248.

2. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 308-318.

3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. –С.245-267.

4. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/ Ред. В.И. Єрмаков. –М.: Инфра-М, 2008. –С.-79-97.

5. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип.–М.: Новое знание,2007. С.121-143.

6. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М.К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 110-113.

7. Прикладные задачи теории вероятности/ Е.С. Вентцель, Л.А. Овчаров. –М.: Радио и связь, 1983. –С.458-462.

8. Статистика (з програмованою формою контролю знань): математична статистика. Загальна теорія статистики: Навчальний посібник для студентів вузів/ А.Т. Опря. -К.: Центр навчальної літератури, 2005. –С. 74-101.

9. Практикум з математичної статистики: Навчальний посібник для студентів вузів/ А.Т. Мармоза. –К.: Кондор, 2004. –С.65-100.

Методичні рекомендації

При підготовці даної теми з’ясувати сутність таких понять як точкова оцінка, інтервальна оцінка, надійність надійний (довірчий) інтервал, рівень значущості. Знати загальний вигляд довірчих інтервалів для математичного сподівання при відомому та невідомому середньому квадратичному відхиленні, для дисперсії. Вміти дати пояснення всіх позначень з формул, а також правила знаходження критичних точок за відповідними таблицями.

 

Задачі для самоконтролю

Задача 1. Випадкова величина Х має нормальний закон розподілу з відомим середнім квадратичним відхиленням і середнім квадратичним відхиленням . Знайти надійний інтервал для оцінки невідомого математичного сподівання, якщо , а .

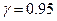Відповідь: 2,72< a <3,68.

Задача 2. Кількісна ознака Х генеральної сукупності розподілена нормально. По вибірці обсягу n=16 знайдені вибіркова середня і виправлене середнє квадратичне відхилення . Оцінити невідоме математичне сподівання за допомогою інтервалу довір’я з надійністю 0,95.

Відповідь: 19,74< a <20,63.

Задача 3. Кількісна ознака Х генеральної сукупності розподілена нормально. По вибірці обсягу n=16 знайдене виправлене середнє квадратичне відхилення . Знайти надійні інтервали для дисперсії при надійності .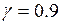

Відповідь: .


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)