АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция

Теорема

Читайте также:
  1. S-M-N-теорема, приклади її використання
  2. Внешние эффекты (экстерналии). Теорема Коуза.
  3. Внешние эффекты, их виды и последствия. Теорема Коуза
  4. Вопрос 1 теорема сложения вероятностей
  5. Вопрос 24 Теорема Остроградского-Гаусса для электрического поля в вакууме
  6. Вопрос. Теорема Котельникова (Найквиста)
  7. Второй закон термодинамики. Энтропия. Закон возрастания энтропии. Теорема Нернста. Энтропия идеального газа.
  8. Гранична теорема Пуассона
  9. Дискретизація сигналу – теорема відліків (Котельникова)
  10. Друга теорема економіки добробуту та її значення
  11. Друга теорема розвинення
  12. Заняття 3. Потік вектора напруженості електричного поля. Теорема Гауса

 

 

Ймовірність настання принаймні однієї з подій

А1, А2,..., Ап, незалежних в сукупності,

знаходиться за формулою

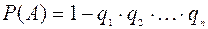(5)


 

Задача 15. Людина може захворіти на грип при попаданні в організм однієї вірусної клітини. Знайти ймовірність того, що людина захворіє на грип, якщо в її організм попаде чотири різні вірусні клітини з ймовірністю потрапити відповідно 0,3; 0,4; 0,6; 0,7.

Розв’язання. За умовою задачі, людина захворіє на грип при попаданні в організм принаймні однієї з чотирьох вірусних клітин. Це дає підстави для використання формули (5). Відомі ймовірності потрапляння в організм людини вірусних клітин, а саме: , , , , відповідно , , 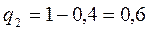, . Отже, підставивши знайдені значення у формулу , маємо: .

Відповідь: 0,9664.

 

Запитання для самоконтролю

1. Що таке ймовірність події? В яких випадках використовують класичне та геометричне означення ймовірності?

2. Що таке відносна частота події?

3. Назвати основні властивості ймовірності та відносної частоти.

4. Сформулювати теореми додавання ймовірностей для несумісних та сумісних подій.

5. Дати означення залежних та незалежних випадкових подій, умовної ймовірності випадкової події.

6. Сформулювати і записати теореми множення ймовірностей залежних та незалежних подій.

 


1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 83 | 84 | 85 |

Поиск по сайту:

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)