 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Сполуки без повторень елементів
Означення. Розміщеннями з n елементів по k (k≤n) називають такі упорядковані сполуки, які складаються з k елементів, взятих з n елементів і відрізняються одна від іншої елементами або їх порядком.
Розглянемо модельні приклади (рис. 2), які допоможуть розкрити нам сутність розміщень.
Приклад. Скількома способами можна розкласти k пронумерованих кульок в n пронумерованих корзин (k≤ n), так, щоб в кожній корзині виявилось не більше однієї кульки.
Розв’яжемо задачу спочатку для n =4, k =2.
Розглянемо рисунок справа: першу кульку ми можемо покласти у будь-яку з чотирьох корзин, після чого другу кульку можна розмістити у будь-яку з трьох корзин, що залишилися. Такі міркування показують, що варіантів може бути 4·3=12, тобто можливими є 12 розміщень.
Розглянемо рисунок зліва: можна представити вибір у вигляді дерева, кожна гілка якого закінчується одним із варіантів розміщень.
Число розміщень з n елементів по k позначається 
і обчислюється за формулою: 
Зауваження. 
0!=1.
Рис. 2
Задача 1. З 9 студентів потрібно обрати старосту, культорга та профорга. Скількома способами це можна зробити?
Розв’язання. Шукане число способів обчислюється за формулою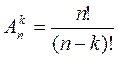 
, оскільки порядок об’єктів важливий.
Отже, 
.
Відповідь: 504 способами.
Розглянемо випадок коли k=n.
Означення. Розміщенняз n елементів по n називаються перестановками.
Різні перестановки відрізняються лише порядком елементів. Число перестановок з п елементів позначається Рп і обчислюється за формулою
Рп=п!, оскільки 
Задача 2. Скільки трицифрових чисел можна скласти з цифр 1,2,3, якщо повторення цифр у числах заборонено?
Розв’язання. Шукана кількість чисел обчислюється за формулою Рп=п!, у даному випадку п = 3, отже Р3= 3! = 1·2·3=6.
Відповідь: 6 чисел.
Означення. Сполученням (комбінацією) з n елементів по k називають такі неупорядковані сполуки, які складаються з k елементів, взятих зданих n елементів і відрізняються одна від іншої принаймні одним елементом.
Дамо відповідь на запитання: „Скількома способами можна вибрати з п різних предметів к штук?”. Розглянемо цю ситуацію для n =4, k =2, наприклад, скількома способами можна вибрати з чотирьох пронумерованих корзин дві.
Розглянемо рис. 2. Вибрані корзини будемо відрізняти тим, що кластимемо в них пронумеровані кульки. Однак, як бачимо, кожний вибір пари корзин зустрічається в 12 розміщеннях двічі. Перший вибір знаходимо у першому рядку та в четвертому, другий – у другому та сьомому, третій – у третьому та десятому, і т.д. Отже, вибрати дві корзини з чотирьох можна шістьма способами 12:2=6 або 
.
Для того, щоб підрахувати скількома способами можна вибрати к корзин з різних п корзин, спочатку обчислюємо кількість розміщень (к різних кульок в п корзинах) 
і одержане число ділимо на кількість кульок в к корзинах, або на кількість перестановок з к.
Число комбінацій з n елементів по k позначається 
і обчислюється за формулою: 
.
Для обчислень доцільно знати, що
1) 
;
2) 
;
3) 
.
Задача 3. Скількома способами можна вибрати 2 деталі з ящика, що містить 10 деталей?
Розв’язання. Шукана кількість способів обчислюється за формулою 
, оскільки порядок елементів не важливий. Отже, 
.
Відповідь: 45 способами.
Поиск по сайту: