Рівень В. 1. Нехай Х – випадкова величина, яка має біноміальний розподіл з параметрами n та р

1. Нехай Х – випадкова величина, яка має біноміальний розподіл з параметрами n та р. Відомо, що М(Х)=12; D(Х)=4. Тоді кількість випробувань дорівнює

1) 18;

2) 24;

3) 9.

2. Дискретна випадкова величина задана законом розподілу

Математичне сподівання дорівнює:

1) 5400;

2) 5450;

3) 6000.

3. Автобус деякого маршруту йде точно за розкладом в інтервалі 6 хвилин. Знайти ймовірність того, що пасажир, котрий підійшов до зупинки, буде чекати наступного автобуса протягом з хвилин. Якою формулою потрібно скористатися для обрахунку ймовірності?

1) ;

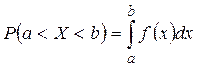2)

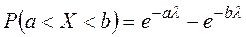
4. Математичне сподівання і середнє квадратичне відхилення нормально розподіленої неперервної випадкової величини Х відповідно рівні 12 і 4. Знайти ймовірність того, що в результаті випробування Х прийме значення з інтервалу (14;16).

Який вираз веде до правильного результату?

1) ;

2) ;

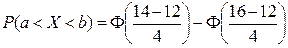3) .

ІІІ. Модульна контрольна робота передбачає розв’язання двох задач, яке оцінюється 2,5 балами.

Орієнтовні варіанти задач для мкр

Поиск по сайту: