Основні принципи комбінаторики

Правило суми. Якщо елемент а можна вибрати із сукупності елементів m способами, а інший елемент b можна вибрати п способами, то вибір „або а, або b ” можна здійснити т+п способами.

Задача 7. У вазі стоять 10 троянд червоного кольору і 5 – рожевого. Скількома способами можна витягти з вази три квітки одного кольору?

Розв’язання. Шукане число способів дорівнює

.

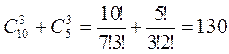Відповідь: 130 способами.

Правило добутку. Якщо елемент а можна вибрати із сукупності елементів m способами і після кожного такого вибору інший елемент b можна вибрати п способами, то вибір пари (а,b) можна здійснити т·п способами.

Задача 8. У їдальні є три перші страви, п’ять других і дві треті страви. Скількома способами можна скласти з них комплексний обід?

Розв’язання. Шукане число способів, згідно з правилом множення, дорівнює 3·5·2=30.

Відповідь: 30 способами.

Запитання для самоконтролю

1. Що є предметом вивчення комбінаторики?

2. Що називають сполукою?

3. Які сполуки називають упорядкованими?

4. У чому різниця між сполуками з повтореннями та без повторень? Наведіть приклади таких сполук.

5. Які сполуки називають розміщеннями, перестановками, комбінаціями? За якими формулами обчислюють кількість цих сполук?

6. Назвіть основні принципи комбінаторики.

Поиск по сайту: