Числові характеристики статистичного розподілу

На практиці часто замість повного вивчення даних вибірки буває достатньо обмежитися знаходженням їх числових характеристик.

По аналогії з числовими характеристиками ДВВ визначають вибіркові числові характеристики, замінюючи при цьому імовірності p_i відносними частотами .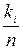

Числові характеристики, обчислені за вибіркою називаються статистиками.

Числові характеристики, обчислені за генеральною сукупностю називаються параметрами.

Наведемо основні статистики.

Означення. Мода – це значення, яке в статистичному ряді зустрічається найчастіше (М₀).

Правило обчислення моди: якщо всі значення в ряді зустрічаються однакову кількість разів, то цей ряд моди немає; якщо два сусідні значення зустрічаються однакову кількість разів, то мода дорівнює їх середньому арифметичному; якщо два несусідні значення зустрічаються однакову кількість разів, то ряд має дві моди і називається бімодальним, а якщо більше двох, то полімодальним.

Для інтервального варіаційного ряду розподілу з однаковими інтервалами моду обчислюють за формулою Орженцького:

,

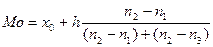де - нижня межа модального інтервалу, т.т. такого, що має найбільшу частоту.

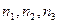- частоти передмодального, модального, післямодального інтервалу відповідно.

- довжина інтервалу.

Означення. Медіана – це значення, яке займає центральне місце у впорядкованому ряді розподілу (М_е).

Правило обчислення медіани: для дискретного впорядкованого варіаційного ряду з непарним числом елементів медіану знаходять як варіанту х з порядковим номером , тобто .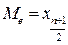

Для ряду з парним числом елементів медіану розраховують як середню арифметичну двох варіант з порядковими номерами та : .

Для інтервального ряду розподілу медіану обчислюють за формулою: , де - нижня межа медіанного інтервалу, 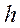– довжина медіанного інтервалу, 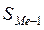– сума частот накопичених перед медіанним інтервалом, – половина суми частот, – частота медіанного інтервалу.

Примітка: медіанний інтервал визначається як інтервал, для якого накопичена частота дорівнює півсумі всіх частот ряду, або перевищує її.

Означення. Вибірковою середньою статистичного розподілу вибірки називають середню арифметичну значень її варіант з урахуванням їхніх частот , тобто

.

Вибіркова середня є основною характеристикою статистичного розподілу вибірки та аналогом математичного сподівання. ЇЇ узагальненням є поняття початкового емпіричного моменту.

Означення. Початковим емпіричним моментом s -того порядку М_s статистичного розподілу вибірки називається середнє арифметичне значення степенів порядку s варіант , тобто .

Розглянемо основні характеристики розсіювання значень вибірки навколо її середнього значення.

Означення. Розмахом вибірки R називають різницю між найбільшим та найменшим значеннями її варіант, тобто .

Означення. Вибірковою дисперсієюD_В статистичного розподілу вибірки називають середню арифметичну квадратів відхилень варіант від вибіркової середньої, тобто .

Для обчислення вибіркової дисперсії часто зручніше використовувати формулу .

Розмірність дисперсії дорівнює квадрату розмірності значень вибірки, що створює незручність у дослідженнях. Щоб її усунути, за характеристику розсіювання значень випадкової величини за результатами значень вибірки приймають вибіркове середнє квадратичне відхилення вибірки s_В, яке визначається рівністю:

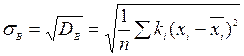
Означення. Коефіцієнтом варіаціїV статистичного розподілу вибірки називається відношення середнього квадратичного відхилення до середньої арифметичної вираженого у відсотках.

Обчислюється за формулою:

.

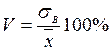Означення. Центральним емпіричним моментом s -того порядку т_s статистичного розподілу вибірки називається середнє арифметичне значення степенів порядку s відхилень варіант від середньої вибіркової , тобто:

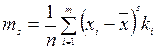
Зокрема, т ₁=0, т ₂= D _В

Для оцінки відхилення статистичного розподілу вибірки від нормального розподілу використовують числові характеристики – асиметрію та ексцес.

Означення. Асиметрією А_В називають число, яке обчислюється за формулою:

де т ₃ – центральний емпіричний момент 3-го порядку, s _В – середнє квадратичне відхилення статистичного розподілу вибірки.

Означення. Ексцесом Е_В статистичного розподілу вибірки називається число, яке обчислюється за формулою:

де т ₄ – центральний емпіричний момент 4-го порядку, s _В – середнє квадратичне відхилення статистичного розподілу вибірки.

Якщо випадкова величина Х розподілена за нормальним законом, то її асиметрія і ексцес дорівнюють нулю.

Усі вищезазначені формули можуть бути використані при обчисленні числових характеристик вибірки для випадку, коли емпіричні дані згруповані за допомогою інтервального варіаційного ряду, зокрема, якщо вважати, що – середини інтервалів.

Обчислення 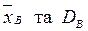можна спростити, використовуючи метод добутків, в основі якого лежать рівновіддалені варіанти та наступна розрахункова таблиця

Поиск по сайту: