Алгебра випадкових подій

Під алгеброю випадкових подій розуміють виконання математичних операцій (дій) над ними. Алгебра подій будується по аналогії з теорією множин.

Нехай А та В випадкові події.

Означення. Сумою (об’єднанням) подій А та В називається випадкова подія А+В (або А È В), яка настає тоді, коли настає принаймні одна з подій А або В.

Сприятливими для суми є елементарні події, які сприятливі або для А, або для В, або для обох подій А і В.

Якщо А та В несумісні, то А È В означає появу події А або події В.

Аналогічно визначають суму більшої кількості подій.

Приклад. Випробування – відзначання Пасхи:

подія А – у березні;

подія В – у квітні;

подія С – у травні.

Тоді випадкова подія А È В È С – відзначання Пасхи відбувається навесні.

Означення. Добутком (перетином) подій А та В називається випадкова подія А·В (або А Ç В), яка настає тоді, коли настають обидві події А і В.

Сприятливими для добутку А·В є елементарні події, які сприятливі і для А, і для В.

Якщо А та В несумісні, то добуток А Ç В є множина, яка немає жодного елемента, тобто А Ç В =Æ.

Аналогічно визначають добуток більшої кількості подій.

Приклад. Випробування – перехід студента з I курсу на II курс:

подія А – студент склав іспит з психології;

подія В – студент склав іспит з математичної статистики;

подія С – студент склав залік з філософії.

Тоді випадкова подія А Ç В Ç С – студент перейшов на II курс.

Означення. Різницею подій А і В називається подія А-В (А\В), яка настає тоді, коли настає подія А і не настає подія В.

Сприятливими для різниці є елементарні події, які сприятливі тільки для А і не сприятливі для В.

Приклад. Випробування – відбір студентів для художнього гуртка:

подія А – студент вміє малювати і грати на музичних інструментах;

подія В – студент вміє грати на музичних інструментах;

Тоді випадкова подія А\В – кількість відібраних студентів для художнього гуртка.

Наведені означення зручно ілюструвати за допомогою діаграм Вена-Ейлера, на яких простір елементарних подій 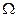зображений у вигляді прямокутника, а події у вигляді кругів (рис. 1).

Рис. 1

Поиск по сайту: