Тема 1. Основні поняття теорії ймовірностей

1.1. Поняття "випробування" та "подія". Предмет теорії ймовірностей. Коротка історична довідка.

В теорії ймовірностей розглядаються експерименти, які в незмінних умовах можна повторити будь-яку кількість разів, але результати яких наперед неможливо передбачити. Такі експерименти називають випробуваннями. Найпростіший результат випробування називається елементарною подією і позначається .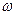

Означення. Сукупність усіх елементарних подій випробування називається простором елементарних подій і позначається .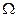

Приклад. Випробування – підкидання монети; елементарні події: 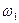–поява герба, 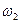– поява номіналу; = .

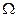Означення. Будь-яка підмножина А простору елементарних подій називається випадковою подією. Елементарні події, що входять в А, називаються сприятливими для А.

Отже, випадковою називають таку подію, яка при умовах, що розглядаються, може здійснитися, а може й не здійснитися.

Випадкові події позначають великими літерами, наприклад, A, B, C, X, Y, Z, A₁, A₂, A₃,…, A_n.

Приклад. Випробування – підкидання правильного грального кубика. Випадкова подія А – поява парного числа очок, тоді А ={ 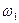, , 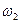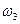}, де 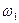– випадання двох очок, 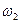– випадання чотирьох очок, 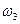– випадання шести очок – сприятливі елементарні події для А.

Окрім випадкових подій розрізняють достовірні та неможливі події.

Означення. Достовірною називають таку подію, яка в даному випробуванні обов’язково здійсниться.

Приклад. Простір елементарних подій 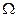– є достовірною подією, оскільки одна з елементарних подій обов’язково здійсниться. У прикладі про підкидання монети обов’язково з’явиться герб або номінал.

Означення. Неможливою називають таку подію, яка в даному випробуванні не може здійснитися.

Приклад. Порожня множина Æ є неможливою подією. У першому прикладі подія „монета впаде на ребро” – неможлива.

Якщо випадкову подію розглядати багато разів при однакових умовах, то можна виявити певну закономірність її появи. Таку закономірність називають імовірною закономірністю масових однорідних випадкових подій.

У теорії ймовірностей під масовими однорідними випадковими подіями розуміють такі події, які здійснюються багатократно при однакових умовах або багато однакових подій.

У XVIII ст. Бюффон підкинув монету 4040 разів. Герб випав 2048 разів. У ХХ ст. Пірсон підкинув монету 24000 разів. Герб випав 12012 разів. Отже, випадання герба є однаково ймовірностним і приблизно дорівнює 0,5.

Означення. Теорія ймовірностей – це наука, яка вивчає закономірності випадкових явищ.

Перші роботи, в яких з’явилися основні поняття теорії ймовірностей, належать вченим XV-XVI століття: Б.Спінозі, Дж. Кардано, Галілео Галілею. Вони будувалися на теорії азартних ігор (наприклад, грі в кості).

Подальшим розвитком (кінець XVII - початок XVIII ст.) теорія ймовірностей зобов’язана таким математикам як Б.Паскаль, П Ферма, Х. Гюйгенс, К. Гаус, Я. Бернуллі, С. Пуассон, А. Муавр, П. Лаплас, Т. Бейєс.

Лише наприкінці XIX ст. П.Л. Чебишов та його учні А.А. Марков та А.М. Ляпунов перетворили теорію ймовірностей у математичну науку.

Поиск по сайту: