Перевірка гіпотези про рівність середніх двох сукупностей

Порівняння середніх двох сукупностей має важливе практичне значення. На практиці часто зустрічається випадок, коли середній результат однієї серії експерименту відрізняється від середнього результату другої серії. При цьому постає питання, чи можна пояснити таку різницю середніх випадковими неминучими помилками експерименту чи вона викликана деякими закономірностями.

В психолого-педагогічних дослідженнях задача порівняння середніх часто виникає при контролі, наприклад, рівня знань учнів, що навчалися за різними навчальними програмами або методиками, або в різних умовах і т.і.

Сформулюємо задачу.

Нехай маємо дві сукупності, що характеризуються генеральними середніми і і відомими дисперсіями і необхідно перевірити гіпотезу Н₀ про рівність генеральних середніх, тобто Н₀: = . Для перевірки гіпотези Н₀ із цих сукупностей взяті дві незалежні вибірки об’ємів п₁ і п₂, по яких знайдено вибіркові середні і та вибіркові дисперсії і .

При достатньо великих об’ємах вибірок вибіркові середні і мають наближено нормальний закон розподілу, відповідно і .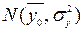

У випадку справедливості гіпотези Н₀ різниця – має нормальний закон розподілу з математичним сподіванням М( – )=М()–М()= – =0 і дисперсією (дисперсія різниці незалежних випадкових величин дорівнює сумі їх дисперсій, а дисперсія середньої п незалежних доданків в п раз менша дисперсії кожного).

Тому при виконанні гіпотези Н₀ статистика

(28)

має стандартний нормальний розподіл .

У випадку альтернативної гіпотези Н₁: > (або Н₁: < ) вибирають односторонню критичну область і критичне значення статистики

(29)

а при конкуруючій гіпотезі Н₁: ¹ вибирають двосторонню критичну область і критичне значення статистики

(30)

Якщо спостережуване значення статистики t більше за t _кр, що визначене на рівні значимості a (за абсолютною величиною), тобто êt ê> t _кр, то гіпотеза Н₀ відхиляється. Якщо êt ê£ t _кр, то робиться висновок, що нульова гіпотеза не протирічить даним спостереження.

Приклад. Для перевірки ефективності нової методики навчання відібрано дві групи студентів. В першій групі чисельністю п₁ =50 студентів, де застосовувалася нова методика, середній бал успішності складав =85 балів, у другій чисельністю п₂ =70 студентів =78 балів. Попередньо встановлено, що дисперсії успішності в групах дорівнюють відповідно =100 і =74. На рівні значимості a=0,05 потрібно з’ясувати вплив нової методики на середній бал успішності студентів.

Розв’язання

Припустимо, що середній бал успішності студентів при викладанні предметів за новою і старою методикою однакові, тобто Н₀: = .

Тоді Н₁: > або Н₂: ¹ (в даній задачі краще взяти Н₁, так як її справедливість означає ефективність застосування нової методики навчання).

За формулою (28) маємо .

При альтернативній гіпотезі Н₁ критичне значення статистики знаходиться з умови (29), тобто , звідки за таблицями значень функції Лапласа t _кр =t _0,9=1,64, а при Н₂ – умова (30), тобто , звідки t _кр =t _0,95=1,96.

Оскільки êt ê> t _кр (при будь-якій із взятих конкуруючих гіпотез), то гіпотеза Н₀ відхиляється, тобто на 5%-ому рівні значимості можна зробити висновок, що нова методика дозволяє підвищити середній бал студентів.

Якщо припустити, що розподіл випадкових величин Х та У в кожній сукупності має нормальний закон розподілу, то тоді, якщо дисперсії і відомі, то перевірка гіпотез проводиться так, як описано вище, не тільки для великих але й для малих по об’єму вибірок. Якщо ж дисперсії і невідомі, але рівні, тобто = = , то в якості невідомої величини можна взяти її оцінку – виправлену вибіркову дисперсію

або .

Однак кращою оцінкою для буде дисперсія змішаної сукупності об’єму п₁ + п₂, тобто

,

а оцінкою дисперсії різниці незалежних вибіркових середніх буде .

Доведено, що у випадку справедливості гіпотези Н₀, статистика

(31)

має t-розподіл Стьюдента з k = п₁ + п₂ -2 ступенями вільності. Тому критичне значення статистики t знаходиться за формулами (29) і (30) в залежності від виду критичної області, в яких замість функції Лапласа Ф(t) береться функція q (t; k) для розподілу Стьюдента при k = п₁ + п₂ -2, тобто q (t; k)=1-a. при цьому зберігається те саме правило відхиляння (приймання) гіпотези: гіпотеза Н₀ відхиляється на рівні значимості a, якщо êt ê> t _1-2a;k, (у випадку односторонньої критичної області) або êt ê> t _1-a;k (у випаду двосторонньої критичної області). У протилежному випадку гіпотеза Н₀ приймається.

Зауваження. Якщо дисперсії = невідомі і не передбачається, що вони рівні, то статистика, обрахована за формулою (31) також має t‑розподіл Стьюдента, однак відповідне йому число ступенів вільності визначається наближено і складніше.

Приклад. Зроблено дві вибірки врожаю пшениці: при своєчасному зборі врожаю і зборі з деяким запізненням. У першому випадку при спостереженні 8 ділянок вибіркова середня урожаю склала 16,2ц/га, а середнє квадратичне відхилення – 3,2ц/га; у другому випадку при спостереженні 9 ділянок ті ж характеристики дорівнювали 13,9ц/га і 2,1ц/га. На рівні значимості a=0,05 з’ясувати вплив своєчасного збору врожаю на середнє значення урожайності.

Розв’язання

Припустимо, що середнє значення урожайності при своєчасному зборі урожаю і з запізненням рівні, тобто Н₀: = .

Тоді Н₁: > , що означає значний вплив на урожайність строків збору. За формулою (31) , k =8+9-2=15 з умови q (t; k)=1-2a=1-2·0,05=0,9. Звідси за таблицею значень критерію Стьюдента (додаток 5) t_0,9;15=1,75. Оскільки <t_0,9;15=1,75, то гіпотеза Н₀ приймається. Це означає, що дані які ми маємо на 5%-ому рівні значимості, не дозволяють вважати, що деяке спізнення у строках збору суттєво впливає на величину урожаю.

Порівняння середніх декількох сукупностей буде розглянуте у темі 11.

Поиск по сайту: