Практичні заняття. Практичне заняття № 15-16 (4 год)

Практичне заняття № 15-16 ( 4 год )

Тема: Перевірка статистичних гіпотез.

Мета: сформувати у студентів уявлення про статистичні гіпотези, навчити обчислювати статистики, знаходити критичні області, застосовувати критерії прийняття нульової та альтернативної гіпотез.

План Заняття

1. Статистичні гіпотези та їх різновиди. Похибки перевірки гіпотез.

2. Статистичний критерій перевірки нульової гіпотези. Основні принципи побудови критичної області.

3. Перевірка гіпотези про нормальний закон розподілу генеральної сукупності. Критерій згоди Пірсона.

4. Перевірка гіпотези про рівність середніх двох нормальних генеральних сукупностей при відомих та невідомих дисперсіях.

5. Перевірка гіпотези про рівність дисперсій двох нормальних генеральних сукупностей.

6. Перевірка гіпотези про рівність часток ознаки двох нормальних генеральних сукупностей.

7. Перевірка гіпотез про числові значення параметрів.

Рекомендована Література

1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 249-264.

2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С.343-365.

3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 330-379.

4. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. –С-268-310.

5. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/Ред. В.И. Єрмаков –М. Инфра-М,2008–С.98-101.

6. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип.–М.: Новое знание, 2007.С.144-150.

7. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М. К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С.114-118.

8. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С.284-298.

9. Математична статистика: Навчальний посібник для студентів вузів/ В.К. Гаркавий, В.В. Ярова. –К.: Профессионал, 2004. –С. 137-147.

10. Статистика (з програмованою формою контролю знань): математична статистика. Загальна теорія статистики: Навчальний посібник для студентів вузів/ А.Т. Опря. -К.: Центр навчальної літератури, 2005. –С. 129-134.

11. Практикум з математичної статистики: Навчальний посібник для студентів вузів/ А.Т. Мармоза. –К.: Кондор, 2004. –С. 101-148.

12. Математические методы психологического исследования. Анализ и интерпретация данных. Учебное пособие. 3-е изд., / Наследов А.Д. –СПб.: Речь, 2007. – С.93-146.

Методичні вказівки

При підготовці даної теми вивчити означення таких понять як статистична гіпотеза, нульова гіпотеза, альтернативна (конкуруюча) гіпотеза, статистичний критерій, критична область, область прийняття гіпотези, критична точка. Знати у чому полягають помилки першого та другого роду, які можуть бути зроблені при перевірці гіпотез. Звернути увагу на односторонню (правосторонню, лівосторонню) та двосторонню критичні області, вміти їх будувати на числовій прямій. Вміти знаходити критичні точки за таблицями різних розподілів. Вивчити алгоритми перевірки та умови прийняття нульової гіпотези при різних варіантах альтернативних гіпотез при перевірці гіпотез, що зазначені у плані заняття.

задачі для самоконтролю

Задача 1. При рівні значущості перевірити гіпотезу про нормальний розподіл генеральної сукупності, якщо відомі емпіричні і теоретичні частоти

Відповідь: розбіжність емпіричних та теоретичних частот незначуща. Отже, генеральна сукупність розподілена нормально.

Задача 2. За двома незалежними вибірками обсягу і знайдені середні розміри деталей відповідно =182мм і =185мм, виготовлених на першому і другому автоматах. Встановлено, що розмір деталі, виготовленої кожним автоматом, має нормальний закон розподілу. Відомі дисперсі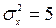ї і 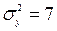для першого і другого автоматів. На рівні значимості 0,05 виявити вплив на середній розмір деталі автомату, на якому вона виготовлена. Розглянути два випадки: а) 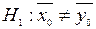; б) . Відповідь: а) вплив суттєвий, оскільки t=2,82>t_0.95=1,96 (двохсторонній критерій); б) вплив суттєвий, оскільки t=2,82>t_0.9=1,64.

Задача 3. За двома незалежними вибірками обсягу 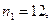вибраним з генеральних сукупностей Х та У, знайдені виправлені вибіркові дисперсії . Перевірити нульову гіпотезу про рівність генеральних дисперсій при альтернативній гіпотезі а) при рівні значущості ; б) при рівні значущості .

Відповідь: а) немає підстав відхиляти нульову гіпотезу про рівність дисперсій генеральних дисперсій. б) немає підстав відхиляти нульову гіпотезу про рівність дисперсій генеральних дисперсій.

Задача 4. За вибіркою об’єму n =20 знайдено виправлену дисперсію . При рівні значущості перевірити нульову гіпотезу про рівність дисперсії гіпотетичному значенню при альтернативній гіпотезі а) ; б) ; в) , якщо .

Відповідь: а) немає підстав відхиляти нульову гіпотезу; б) приймаємо нульову гіпотезу; в) приймаємо нульову гіпотезу.

Задача 5. Вступний екзамен проводився на двох факультетах університету. На природничому факультеті із n ₁=900 абітурієнтів склали екзамен 500 чоловік; а на психолого-педагогічному факультеті із n ₁=800 абітурієнтів склали екзамен 408 чоловік. на рівні значимості 0,05 перевірити гіпотезу про відсутність суттєвої різниці в рівні підготовки абітурієнтів для двох факультетів. Розглянути два випадки: а) ; б) .

Поиск по сайту: