 |
АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомДругоеЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция
Практичне заняття №6
Тема: Дискретні випадкові величини.
Мета: сформувати знання про випадкові величини, їх закони розподілу, числові характеристики.
Основні знання, якими повинні оволодіти студенти під час вивчення теми: знати основні закони розподілу ДВВ, формули для обчислення основних числових характеристик (математичне сподівання, дисперсія, середнє квадратичне відхилення).
Основні вміння, якими повинні оволодіти студенти під час вивчення теми: вміти будувати закони розподілу ДВВ, а також визначати їх числові характеристики, будувати функцію розподілу ДВВ.
План ЗАняття
1. Види випадкових величин та способи їх задання.
2. Закони розподілу ДВВ.
3. Числові характеристики ДВВ.
Рекомендована література
1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 93-113.
2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С. 240-245.
3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 87-173.
4. Теорія ймовірностей...від найпростішого: Навчальний посібник для студентів вузів/ О. Д. Валь, К.С. Королюк, С.В. Мельничук. –Чернівці: Книги-ХХІ, 2004.-С. 69-98.
5. Основи теорії ймовірностей: курс лекцій: Навч. посібник/ В.М. Рабик. – Львів: Магнолія плюс, 2004. С. 39-104.
6. Курс теории вероятностей: Учебник для студентов вузов / В.П. Чистяков. – 7-е изд.,исп. и доп. –М: Дрофа, 2007.- С.71-107.
7. Теорія ймовірностей: основні поняття, приклади, задачі: Навчальний посібник/В.М. Турчин. – К.: А.С.К., 2004.- С.47-100.
8. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. - С.51-71.
9. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/Ред. В.И. Єрмаков.–М.:Инфра-М, 2008.–С.25-34.
10. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип. –М.: Новое знание, 2007. С. 40-43.
11. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М. К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 40-97.
12. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С. 48-101.
13. Прикладные задачи теории вероятности/ Е.С. Вентцель, Л.А. Овчаров. –М.: Радио и связь, 1983. –С. 82-150.
14. Математична статистика та задачі оптимізації в алгоритмах і програмах: Навчальний посібник для студентів вузів/ Ю.А.Толбатов. –К.: Вища школа, 1994. –С.30-66.
15. Елементи теорії ймовірностей (для студентів заочної форми навчання). Навчальний посіб. (Модуль 2)./ В.М. Резанко. – К.: 2007.-С. 7-66.
Методичні рекомендації
1. Опрацювати рекомендовану літературу.
2. Повторити поняття функції, а також поняття повної групи подій.
3. Вивчити основні закони розподілу, функції розподілу, формули для визначення основних числових характеристик: математичного сподівання, дисперсії, середньоквадратичного відхилення.
задачі для самоконтролю
Задача 1. Проводиться тестування трьох людей. Ймовірність того, що обрана людина виявиться інтровертом – 0,6. Дослідження припиняється при першому виявленні інтроверта. Дискретна випадкова величина – кількість досліджених людей. Знайти закон розподілу випадкової величини, числові характеристики та функцію розподілу.
Відповідь:
Закон розподілу:
| х | |||
| Р | 0,6 | 0,24 | 0,16 |
Числові характеристики: М(Х)=1,56; D(X)=0,5664; 
Функція розподілу: 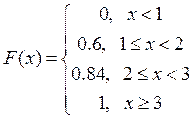 .
.
Задача 2. Туристична агенція має 3 „горящі” путівки до Франції, Італії та Китаю. Ймовірність придбання путівки до Франції дорівнює 0,8, до Італії – 0,9, до Китаю – 0,7. Дискретна випадкова величина – кількість придбаних горящих путівок. Знайти: закон розподілу, числові характеристики та функцію розподілу. Побудувати графік функції розподілу.
Відповідь: закон розподілу
| Х | ||||
| Р | 0,006 | 0,092 | 0,398 | 0,504 |
Числові характеристики:М(Х)=2,4; D(X)=0,46; 
Функція розподілу:  .
.
задача 3. Полиця в шафі розділена на дві частини у співвідношенні 2:1. На цю полицю студент ставить три банки з варенням. Ймовірність розстановки банки в будь-яке місце полиці рівноможливе. Дискретна випадкова величина – кількість банок, поставлених на більшу частину полиці. Знайти: закон розподілу, числові характеристики, функцію розподілу випадкової величини.
Відповідь: закон розподілу
| Х | ||||
| Р | 1/27 | 2/9 | 4/9 | 8/27 |
Числові характеристики: М(Х)=2; D(X)=  ;
;  .
.
Функція розподілу:  .
.
Практичне заняття №7-8 (4 год)
Тема: Неперервні випадкові величини.
Мета: сформувати знання про неперервні випадкові величини, їх закони розподілу, числові характеристики
Основні знання, якими повинні оволодіти студенти під час вивчення теми: знати означення диференційованої та інтегральної функцій розподілу, знати основні закони розподілу НВВ, формули для обчислення основних числових характеристик (математичне сподівання, дисперсія, середнє квадратичне відхилення).
Основні вміння, якими повинні оволодіти студенти під час вивчення теми: вміти знаходити диференціальну та інтегральну функції розподілу НВВ, а також визначати їх числові характеристики, застосовувати основні формули для нормально розподілених НВВ.
План
1. Щільність ймовірностей та функція розподілу НВВ.
2. Закони розподілу НВВ.
3. Числові характеристики НВВ.
рекомендована Література
1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 114-124.
2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С. 245-254.
3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 87-173.
4. Теорія ймовірностей...від найпростішого: Навчальний посібник для студентів вузів/ О. Д. Валь, К.С. Королюк, С.В. Мельничук. –Чернівці: Книги-ХХІ, 2004.-С. 69-98.
5. Основи теорії ймовірностей: курс лекцій: Навч. посібник/ В.М. Рабик. – Львів: Магнолія плюс, 2004. С. 39-104.
6. Курс теории вероятностей: Учебник для студентов вузов/ В.П. Чистяков. – 7-е изд.,испр. и доп.–М: Дрофа, 2007.-С.71-107.
7. Теорія ймовірностей: основні поняття, приклади, задачі: Навчальний посібник/В.М. Турчин. – К.:А.С.К., 2004.-С.101-120.
8. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ К.В. Балдин, В.Н. Башлыков, А.В. Рукосуев. –М.: Даликов и К, 2008. - С.51-71.
9. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/Ред. В.И. Єрмаков.–М.:Инфра-М, 2008.–С.35-46.
10. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип. –М.: Новое знание, 2007. С. 44-57.
11. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М. К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 40-97.
12. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С. 48-101.
13. Прикладные задачи теории вероятности/ Е.С. Вентцель, Л.А. Овчаров. –М.: Радио и связь, 1983. –С. 153-173.
14. Математична статистика та задачі оптимізації в алгоритмах і програмах: Навчальний посібник для студентів вузів/ Ю.А.Толбатов. –К.: Вища школа, 1994. –С.30-66.
15. Елементи теорії ймовірностей (для студентів заочної форми навчання). Навчальний посіб. (Модуль 2)./ В.М. Резанко. – К.: 2007.-С. 30-66.
Методичні вказівки
1. Опрацювати рекомендовану літературу.
2. Повторити поняття закону розподілу ДВВ, функції розподілу та числові характеристики для ДВВ.
3. Повторити правила знаходження похідних та первісних від основних функцій.
4. Вивчити означення диференціальної та інтегральної функцій розподілу, знати основні закони розподілу НВВ, формули для обчислення основних числових характеристик.
задачі для самоконтролю
Задача 1. Неперервна випадкова величина Х задана інтегральною функцією розподілу:
 .
.
Знайти диференціальну функцію розподілу, математичне сподівання, дисперсію, а також ймовірність попадання значення випадкової величини в інтервал [0.5;1].
Відповідь:
диференціальна функція 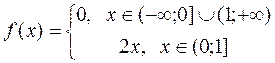 ;
;
числові характеристики: М(Х)=  ; D(X)=
; D(X)=  ;
;
ймовірність попадання значення випадкової величини в інтервал [0,5;1] дорівнює 0,75.
Задача 2. Щільність ймовірності деякої неперервної випадкової величини задана таким чином:  .
.
Визначити параметр А, знайти вираз для густини ймовірності, інтегральну функцію розподілу, математичне сподівання, дисперсію, а також ймовірність того, що випадкова величина прийме значення на інтервалі [0,5;2].
Відповідь:  ; диференціальна функція
; диференціальна функція  ; інтегральна функція розподілу
; інтегральна функція розподілу 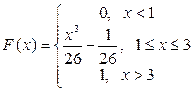 ; числові характеристики: М(Х)=
; числові характеристики: М(Х)=  ; D(X)=0,354; ймовірність попадання значення випадкової величини в інтервал [0,5;1] дорівнює
; D(X)=0,354; ймовірність попадання значення випадкової величини в інтервал [0,5;1] дорівнює  .
.
Задача 3. Діаметр ялинкової кульки – випадкова величина, розподілена за нормальним законом розподілу з математичним сподіванням 5см і дисперсією 0,09см2. Знайти ймовірність того, що розмір діаметру випадково взятої ялинкової кульки відрізняється від математичного сподівання за абсолютною величиною не більше ніж на 0,4см.
Відповідь: 0,816.
Задача 4. Маса сумки з підручниками студента першокурсника – випадкова величина, розподілена за нормальним законом розподілу з математичним сподіванням 5кг і середнім квадратичним відхиленням 0,5кг. Знайти ймовірність того, що маса сумки з підручниками не перевищить 5,5кг.
Відповідь: 0,84
Практичне заняття №9
Тема: Закон великих чисел, центральна гранична теорема, нерівність Чебишова.
Мета: сформувати знання про закон великих чисел, центральну граничну теорему
Основні знання, якими повинні оволодіти студенти під час вивчення теми: знати закон великих чисел, нерівність Чебишова в двох формах, найважливіші граничні теореми: теорема Бернуллі, теорема Чебишова, теорема Ляпунова, центральна гранична теорема.
Основні вміння, якими повинні оволодіти студенти під час вивчення теми: вміти застосовувати закон великих чисел, нерівність Чебишова, граничні теореми для розв’язування практичних задач.
План заняття
1. Загальні поняття про закон великих чисел.
2. Нерівність Чебишова.
3. Граничні теореми.
рекомендована Література
1. Теорія ймовірностей та математична статистика: Навч. посібник для студентів вузів/ В.В. Барковський, Н.В. Барковська Н.В., О.К. Лопатін. 3-є вид. перероб. і доп.– К.: Центр навчальної літератури, 2002. С. 126-131.
2. Математика для психологов: Учебник /А.Н. Киричевец, Е.В. Шикин, А.Г. Дьячков / Под ред. А.Н. Киричевца. – М.:Флинта: Московский психолого-социальный институт, 2003. С. 277-280.
3. Теория вероятностей и математическая статистика: Учебник для студентов вузов/ Н.Ш. Кремер. -3-е изд., перераб. и доп.- М.: Юнити, 2007. – С. 218-236.
4. Теорія ймовірностей...від найпростішого: Навчальний посібник для студентів вузів/ О. Д. Валь, К.С. Королюк, С.В. Мельничук. –Чернівці: Книги-ХХІ, 2004.-С. 115-122.
5. Основи теорії ймовірностей: курс лекцій: Навч. посібник/ В.М. Рабик. – Львів: Магнолія плюс, 2004. С. 105-116.
6. Курс теории вероятностей: учебник для студентов вузов/ В.П. Чистяков. –7-е изд.,испр. и доп.–М:Дрофа, 2007.-С.109-124.
7. Теория вероятностей и математическая статистика: Учебное пособие для студентов вузов/Ред. В.И. Єрмаков.–М.:Инфра-М, 2008.–С.61-73.
8. Теория вероятностей и математическая статистика: примеры и задачи: Учебное пособие для студентов вузов/ И.В. Белько, Г.П. Свирид. -3-е изд., стереотип. –М.: Новое знание, 2007. С. 90-98.
9. Посібник з теорії ймовірності та математичної статистики: Навч. посібник для вузів/ М.К. Бугір. – Тернопіль: Підручники і посібники, 1998. –С. 98-105.
10. Основи теорії ймовірностей та математичної статистики: Навчальний посібник для студентів/ В.П. Бабак, А.Я. Білецький, О.П. Приставка, П.О. Приставка.-К.: КВІЦ.,2003. –С. 157-180.
11. Прикладные задачи теории вероятности/ Е.С. Вентцель, Л.А. Овчаров. –М.: Радио и связь, 1983. –С. 399-429.
12. Математична статистика та задачі оптимізації в алгоритмах і програмах: Навчальний посібник для студентів вузів/ Ю.А.Толбатов. –К.: Вища школа, 1994. –С.80-87.
13. Елементи теорії ймовірностей (для студентів заочної форми навчання). Навчальний посіб. (Модуль 2)./ В.М. Резанко. – К.: 2007.-С. 93-96.
Методичні вказівки
1. Опрацювати рекомендовану літературу.
2. Вивчити форми нерівності Чебишова та з’ясувати її роль у доведенні граничних теорем – Бернулі, Чебишова, центральної граничної теореми та теореми Ляпунова.
задачі для самоконтролю
Задача 1. Дисперсія випадкової величини Х дорівнює 0,001. Яка ймовірність того, що випадкова величина Х відрізняється від її математичного сподівання М(Х) більше ніж на 0,1?
Відповідь: 0,1.
Задача 2. Використовуючи нерівність Чебишова, оцінити ймовірність того, що |X-M(X)|<0,2, якщо D(X)=0,004.
Відповідь: 0,9.
Задача 3. Дано  і D(X)=0,009. Використовуючи нерівність Чебишова, знайти
і D(X)=0,009. Використовуючи нерівність Чебишова, знайти  .
.
Відповідь: 0,3.
Поиск по сайту: